Question-183737

Question Number 183737 by Michaelfaraday last updated on 29/Dec/22

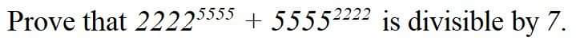
Answered by Frix last updated on 29/Dec/22

mod (2222^(6k) ; 7) =1 mod (2222^(6k+1) ; 7) =3 mod (2222^(6k+2) ; 7) =2 mod (2222^(6k+3) ; 7) =6 mod (2222^(6k+4) ; 7) =4 mod (2222^(6k+5) ; 7) =5 mod (5555^(6k) ; 7) =1 mod (5555^(6k+1) ; 7) =4 mod (5555^(6k+2) ; 7) =2 mod (5555^(6k+3) ; 7) =1 mod (5555^(6k+4) ; 7) =4 mod (5555^(6k+5) ; 7) =2 5555=6k+5 2222=6k+2 ⇒ 2222^(5555) =2222^(6k+5) ⇒ mod (2222^(5555) ; 7) =5 5555^(2222) =5555^(6k+2) ⇒ mod (5555^(2222) ; 7) =2 5+2=7

$$\mathrm{mod}\:\left(\mathrm{2222}^{\mathrm{6}{k}} ;\:\mathrm{7}\right)\:=\mathrm{1} \\ $$$$\mathrm{mod}\:\left(\mathrm{2222}^{\mathrm{6}{k}+\mathrm{1}} ;\:\mathrm{7}\right)\:=\mathrm{3} \\ $$$$\mathrm{mod}\:\left(\mathrm{2222}^{\mathrm{6}{k}+\mathrm{2}} ;\:\mathrm{7}\right)\:=\mathrm{2} \\ $$$$\mathrm{mod}\:\left(\mathrm{2222}^{\mathrm{6}{k}+\mathrm{3}} ;\:\mathrm{7}\right)\:=\mathrm{6} \\ $$$$\mathrm{mod}\:\left(\mathrm{2222}^{\mathrm{6}{k}+\mathrm{4}} ;\:\mathrm{7}\right)\:=\mathrm{4} \\ $$$$\mathrm{mod}\:\left(\mathrm{2222}^{\mathrm{6}{k}+\mathrm{5}} ;\:\mathrm{7}\right)\:=\mathrm{5} \\ $$$$ \\ $$$$\mathrm{mod}\:\left(\mathrm{5555}^{\mathrm{6}{k}} ;\:\mathrm{7}\right)\:=\mathrm{1} \\ $$$$\mathrm{mod}\:\left(\mathrm{5555}^{\mathrm{6}{k}+\mathrm{1}} ;\:\mathrm{7}\right)\:=\mathrm{4} \\ $$$$\mathrm{mod}\:\left(\mathrm{5555}^{\mathrm{6}{k}+\mathrm{2}} ;\:\mathrm{7}\right)\:=\mathrm{2} \\ $$$$\mathrm{mod}\:\left(\mathrm{5555}^{\mathrm{6}{k}+\mathrm{3}} ;\:\mathrm{7}\right)\:=\mathrm{1} \\ $$$$\mathrm{mod}\:\left(\mathrm{5555}^{\mathrm{6}{k}+\mathrm{4}} ;\:\mathrm{7}\right)\:=\mathrm{4} \\ $$$$\mathrm{mod}\:\left(\mathrm{5555}^{\mathrm{6}{k}+\mathrm{5}} ;\:\mathrm{7}\right)\:=\mathrm{2} \\ $$$$ \\ $$$$\mathrm{5555}=\mathrm{6}{k}+\mathrm{5} \\ $$$$\mathrm{2222}=\mathrm{6}{k}+\mathrm{2} \\ $$$$ \\ $$$$\Rightarrow \\ $$$$\mathrm{2222}^{\mathrm{5555}} =\mathrm{2222}^{\mathrm{6}{k}+\mathrm{5}} \:\Rightarrow\:\mathrm{mod}\:\left(\mathrm{2222}^{\mathrm{5555}} ;\:\mathrm{7}\right)\:=\mathrm{5} \\ $$$$\mathrm{5555}^{\mathrm{2222}} =\mathrm{5555}^{\mathrm{6}{k}+\mathrm{2}} \:\Rightarrow\:\mathrm{mod}\:\left(\mathrm{5555}^{\mathrm{2222}} ;\:\mathrm{7}\right)\:=\mathrm{2} \\ $$$$\mathrm{5}+\mathrm{2}=\mathrm{7} \\ $$

Answered by mr W last updated on 29/Dec/22

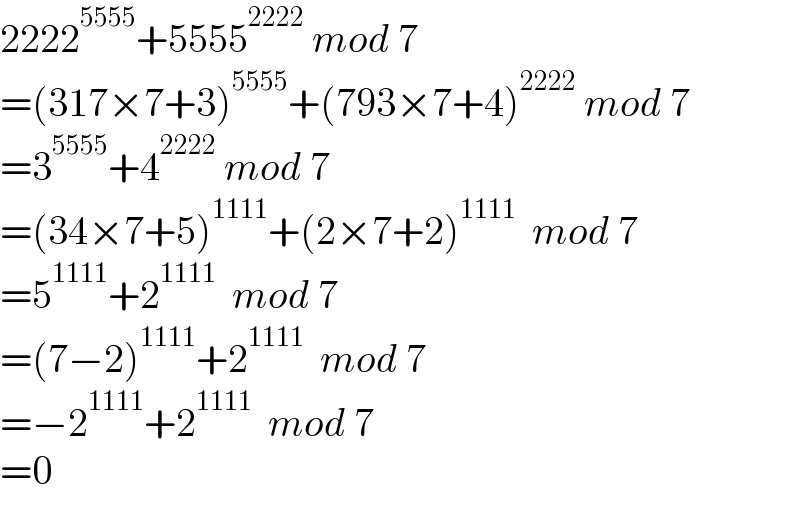
2222^(5555) +5555^(2222) mod 7 =(317×7+3)^(5555) +(793×7+4)^(2222) mod 7 =3^(5555) +4^(2222) mod 7 =(34×7+5)^(1111) +(2×7+2)^(1111) mod 7 =5^(1111) +2^(1111) mod 7 =(7−2)^(1111) +2^(1111) mod 7 =−2^(1111) +2^(1111) mod 7 =0

$$\mathrm{2222}^{\mathrm{5555}} +\mathrm{5555}^{\mathrm{2222}} \:{mod}\:\mathrm{7} \\ $$$$=\left(\mathrm{317}×\mathrm{7}+\mathrm{3}\right)^{\mathrm{5555}} +\left(\mathrm{793}×\mathrm{7}+\mathrm{4}\right)^{\mathrm{2222}} \:{mod}\:\mathrm{7} \\ $$$$=\mathrm{3}^{\mathrm{5555}} +\mathrm{4}^{\mathrm{2222}} \:{mod}\:\mathrm{7} \\ $$$$=\left(\mathrm{34}×\mathrm{7}+\mathrm{5}\right)^{\mathrm{1111}} +\left(\mathrm{2}×\mathrm{7}+\mathrm{2}\right)^{\mathrm{1111}} \:\:{mod}\:\mathrm{7} \\ $$$$=\mathrm{5}^{\mathrm{1111}} +\mathrm{2}^{\mathrm{1111}} \:\:{mod}\:\mathrm{7} \\ $$$$=\left(\mathrm{7}−\mathrm{2}\right)^{\mathrm{1111}} +\mathrm{2}^{\mathrm{1111}} \:\:{mod}\:\mathrm{7} \\ $$$$=−\mathrm{2}^{\mathrm{1111}} +\mathrm{2}^{\mathrm{1111}} \:\:{mod}\:\mathrm{7} \\ $$$$=\mathrm{0} \\ $$

Commented by Michaelfaraday last updated on 29/Dec/22

$${thanks}\:{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply