Question Number 183848 by Michaelfaraday last updated on 30/Dec/22

Commented by MJS_new last updated on 31/Dec/22

$${y}=−{a}\vee{y}=−{b} \\ $$$$\mathrm{look}\:\mathrm{at}\:\mathrm{it},\:\mathrm{it}'\mathrm{s}\:\mathrm{plain}\:\mathrm{to}\:\mathrm{see} \\ $$
Answered by a.lgnaoui last updated on 31/Dec/22
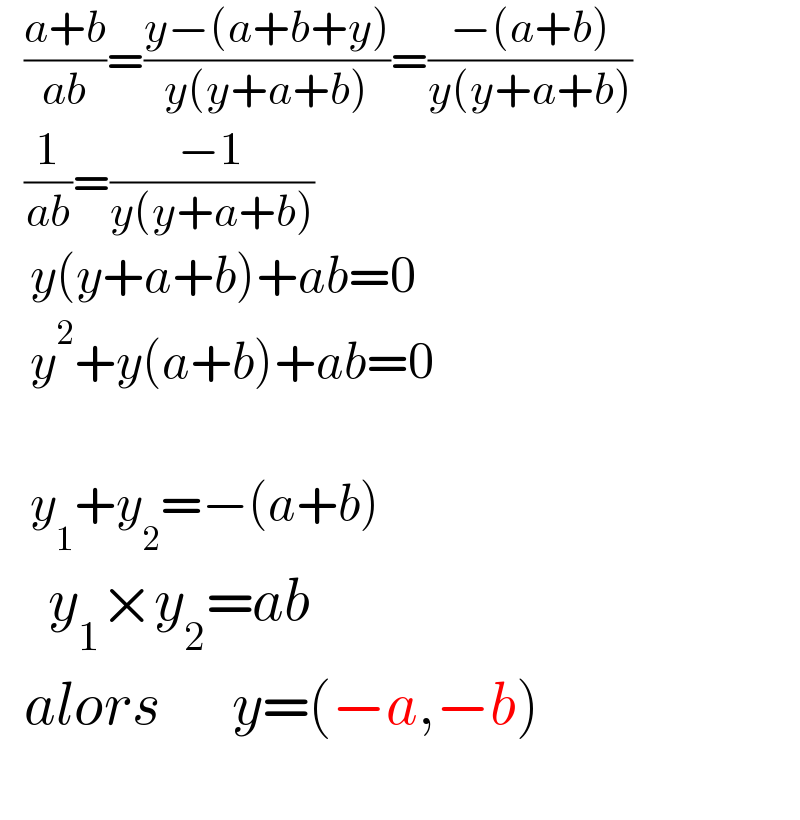
$$\:\:\:\frac{{a}+{b}}{{ab}}=\frac{{y}−\left({a}+{b}+{y}\right)}{{y}\left({y}+{a}+{b}\right)}=\frac{−\left({a}+{b}\right)}{{y}\left({y}+{a}+{b}\right)} \\ $$$$\:\:\:\frac{\mathrm{1}}{{ab}}=\frac{−\mathrm{1}}{{y}\left({y}+{a}+{b}\right)} \\ $$$$\:\:\:{y}\left({y}+{a}+{b}\right)+{ab}=\mathrm{0} \\ $$$$\:\:\:{y}^{\mathrm{2}} +{y}\left({a}+{b}\right)+{ab}=\mathrm{0} \\ $$$$ \\ $$$$\:\:\:{y}_{\mathrm{1}} +{y}_{\mathrm{2}} =−\left({a}+{b}\right) \\ $$$$\:\:\:\:{y}_{\mathrm{1}} ×{y}_{\mathrm{2}} ={ab} \\ $$$$\:\:{alors}\:\:\:\:\:\:{y}=\left(−{a},−{b}\right) \\ $$$$ \\ $$
Commented by Michaelfaraday last updated on 31/Dec/22

$${thanks}\:{sir} \\ $$
Commented by mr W last updated on 31/Dec/22

$${y}^{\mathrm{2}} +{y}\left({a}+{b}\right)+{ab}=\mathrm{0} \\ $$$$\Rightarrow\left({y}+{a}\right)\left({y}+{b}\right)=\mathrm{0} \\ $$$$\Rightarrow{y}=−{a},\:{y}=−{b} \\ $$
Answered by Rasheed.Sindhi last updated on 31/Dec/22

$$\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}=\frac{\mathrm{1}}{{a}+{b}+{y}}−\frac{\mathrm{1}}{{y}} \\ $$$$\:\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{y}}=\frac{\mathrm{1}}{{a}+{b}+{y}}−\frac{\mathrm{1}}{{b}} \\ $$$$\:\:\:\:\:\:\:\frac{{y}+{a}}{{ay}}=\frac{{b}−{a}−{b}−{y}}{{b}\left({a}+{b}+{y}\right)} \\ $$$$\:\:\:\:\:\:\frac{{y}+{a}}{{ay}}+\frac{{a}+{y}}{{b}\left({a}+{b}+{y}\right)}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\left({y}+{a}\right)\left(\frac{\mathrm{1}}{{ya}}+\frac{\mathrm{1}}{{b}\left({a}+{b}+{y}\right)}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:{y}=−{a}\:\vee\:\frac{\mathrm{1}}{{ya}}=−\frac{\mathrm{1}}{{b}\left({a}+{b}+{y}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{ya}=−{ab}−{b}^{\mathrm{2}} −{by} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}\left({a}+{b}\right)=−{b}\left({a}+{b}\right)\:;\:{a}+{b}\neq\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}=−{b}\: \\ $$$${y}=−{a}\:\vee\:{y}=−{b} \\ $$
Commented by mr W last updated on 31/Dec/22
��
