Question-184041

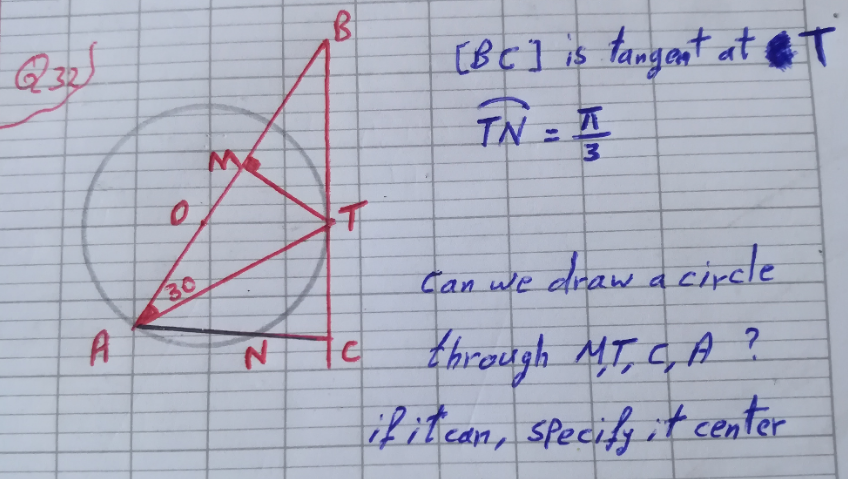
Question Number 184041 by Acem last updated on 02/Jan/23

Answered by HeferH last updated on 02/Jan/23

\overset{⌢}{T N} = \frac{π}{3} = \frac{180 °}{3} = 60 ° \Rightarrow ∠ T A N = \frac{\overset{⌢}{T N}}{2} = 30 °

∠ A O T = 120 ° (△ A O T i s o s c e l e s)

∠ A T C = \frac{\overset{⌢}{A T}}{2} = 60 \Rightarrow ∠ A C T = 90 °

M T C A i s c y c l i c,

t h e c e n t e r w o u l d b e t h e m i d p o i n t o f A T

Answered by mr W last updated on 02/Jan/23

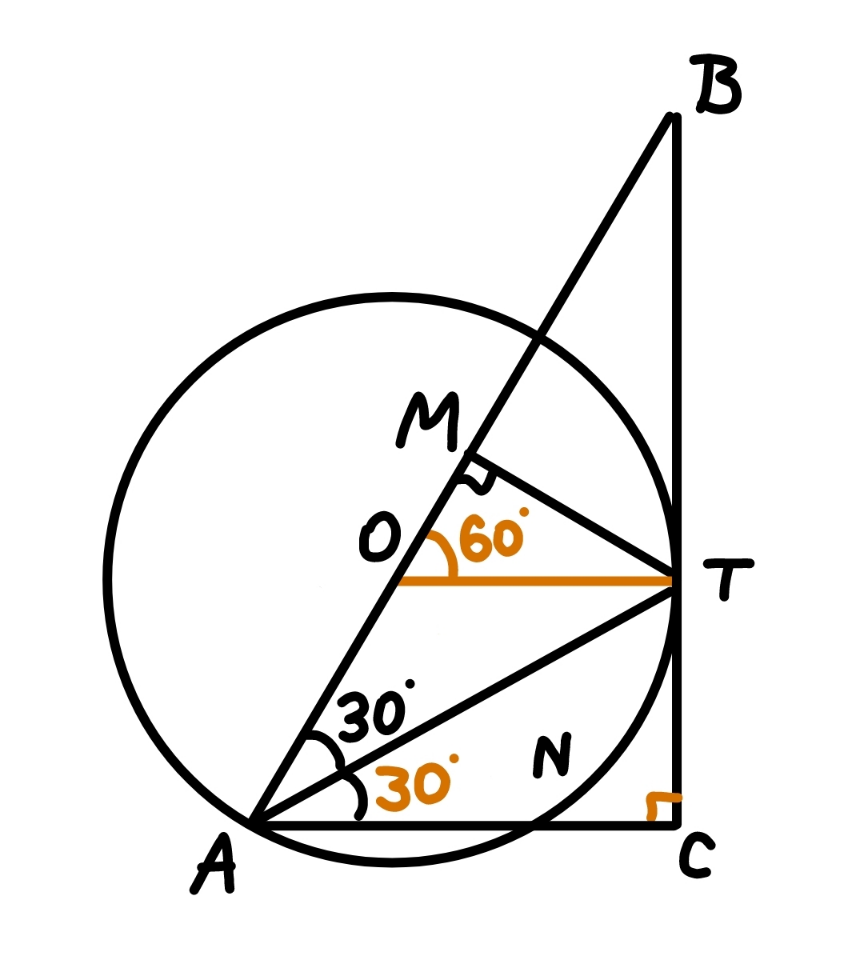
Commented by mr W last updated on 02/Jan/23

∠ T A N = \frac{\overset{⌢}{T N}}{2} = 30 °

∠ B O T = 2 ∠ O A T = 60 ° = ∠ O A C

\Rightarrow A C / / O T

\Rightarrow A C ⊥ B C

\Rightarrow ∠ A C B = 90 ° = ∠ A M T

\Rightarrow A C T M a r e c y c l i c, l i e o n a c i r c l e

w i t h A T a s d i a m e t e r . M i d p o i n t

o f A T i s t h e c e n t e r .

Facebook Tweet Pin