Question-184093

Question Number 184093 by Ib last updated on 02/Jan/23

Answered by manxsol last updated on 03/Jan/23

(1+(t/(100)))^(10) =3 (1+(1/((((100)/t)))))^(10) =3 (1+(1/((((100)/t)))))^(10×((10)/t)) =3^((10)/t) c=3^((10)/t) 1ne=ln(3^((10)/t) ) 1=((10)/t)ln3 t=10ln3 t=10.99 theory _ & calculate lim_(x→∞) (1+(1/x))^x =e e 2.718282 ln3 1.098612 t=10.99 (1+((10.99)/(100)))^(10) 2.836864 no exacto otro metodo 10ln(1+t)=ln3 1+t=(e^(ln3) )^(1/(10)) t=(e^(ln3) )^(1/(10)) −1 t=3^(1/(10)) −1 t=0.116123=(x/(100)) x=11.61 (1+((11.61)/(100)))^(10) 2.999377 ok x=11.61 es la solucion

$$\left(\mathrm{1}+\frac{{t}}{\mathrm{100}}\right)^{\mathrm{10}} =\mathrm{3} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{\left(\frac{\mathrm{100}}{{t}}\right)}\right)^{\mathrm{10}} =\mathrm{3} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{\left(\frac{\mathrm{100}}{{t}}\right)}\right)^{\mathrm{10}×\frac{\mathrm{10}}{{t}}} =\mathrm{3}^{\frac{\mathrm{10}}{{t}}} \\ $$$${c}=\mathrm{3}^{\frac{\mathrm{10}}{{t}}} \\ $$$$\mathrm{1}{ne}=\mathrm{ln}\left(\mathrm{3}^{\frac{\mathrm{10}}{\mathrm{t}}} \right) \\ $$$$\mathrm{1}=\frac{\mathrm{10}}{\mathrm{t}}\mathrm{ln3} \\ $$$${t}=\mathrm{10}{ln}\mathrm{3} \\ $$$$\mathrm{t}=\mathrm{10}.\mathrm{99} \\ $$$$\mathrm{theory}\:_{} \&\:{calculate} \\ $$$${lim}_{{x}\rightarrow\infty} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{x}} =\mathrm{e} \\ $$$$\mathrm{e} \\ $$$$\mathrm{2}.\mathrm{718282} \\ $$$$\mathrm{ln3} \\ $$$$\mathrm{1}.\mathrm{098612} \\ $$$$\mathrm{t}=\mathrm{10}.\mathrm{99} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{10}.\mathrm{99}}{\mathrm{100}}\right)^{\mathrm{10}} \\ $$$$\mathrm{2}.\mathrm{836864}\:\:{no}\:{exacto} \\ $$$${otro}\:{metodo} \\ $$$$\mathrm{10}{ln}\left(\mathrm{1}+{t}\right)={ln}\mathrm{3} \\ $$$$\mathrm{1}+{t}=\left({e}^{{ln}\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{10}}} \\ $$$${t}=\left({e}^{{ln}\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{10}}} −\mathrm{1} \\ $$$${t}=\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{10}}} −\mathrm{1} \\ $$$${t}=\mathrm{0}.\mathrm{116123}=\frac{{x}}{\mathrm{100}} \\ $$$${x}=\mathrm{11}.\mathrm{61} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{11}.\mathrm{61}}{\mathrm{100}}\right)^{\mathrm{10}} \\ $$$$\mathrm{2}.\mathrm{999377}\:\:{ok}\:\:{x}=\mathrm{11}.\mathrm{61} \\ $$$$\:{es}\:{la}\:{solucion} \\ $$$$ \\ $$

Commented by Frix last updated on 03/Jan/23

We don′t need all this. The exact value is (1+(t/(100)))^(10) =3 ⇔ 1+(t/(100))=±(3)^(1/(10)) ⇔ t=100(±(3)^(1/(10)) −1)

$$\mathrm{We}\:\mathrm{don}'\mathrm{t}\:\mathrm{need}\:\mathrm{all}\:\mathrm{this}.\:\mathrm{The}\:\mathrm{exact}\:\mathrm{value}\:\mathrm{is} \\ $$$$\left(\mathrm{1}+\frac{{t}}{\mathrm{100}}\right)^{\mathrm{10}} =\mathrm{3}\:\Leftrightarrow\:\mathrm{1}+\frac{{t}}{\mathrm{100}}=\pm\sqrt[{\mathrm{10}}]{\mathrm{3}}\:\Leftrightarrow\:{t}=\mathrm{100}\left(\pm\sqrt[{\mathrm{10}}]{\mathrm{3}}−\mathrm{1}\right) \\ $$

Commented by manolex last updated on 03/Jan/23

$${true},{is}\:{exact} \\ $$

Commented by manolex last updated on 03/Jan/23

$${t}_{\mathrm{1}} =\mathrm{11}.\mathrm{61}\:\:\:\:\:{t}_{\mathrm{2}} =−\mathrm{211}.\mathrm{61} \\ $$

Answered by manxsol last updated on 02/Jan/23

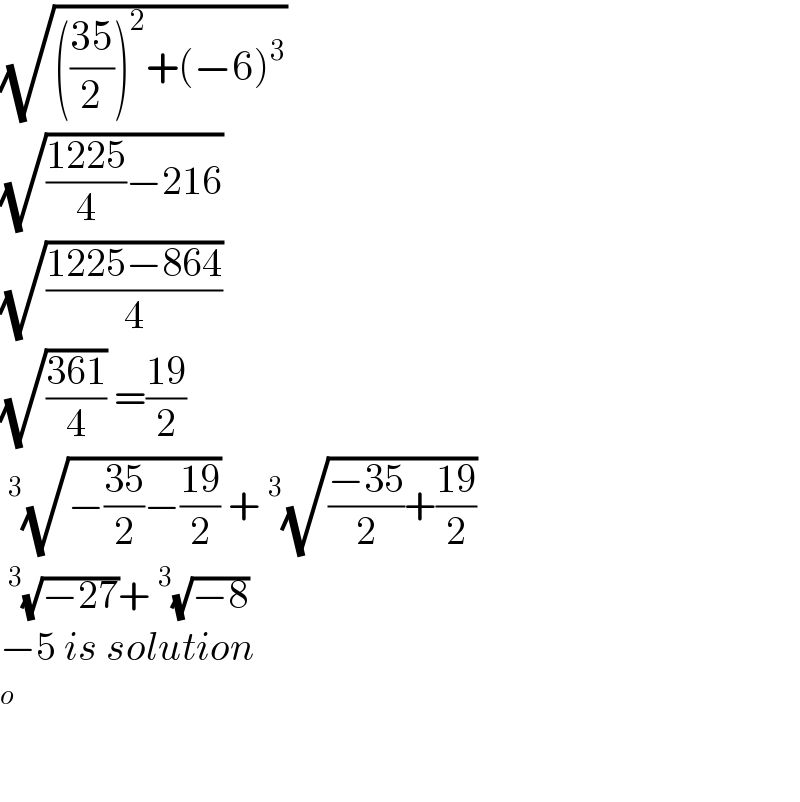
(√((((35)/2))^2 +(−6)^3 )) (√(((1225)/4)−216)) (√((1225−864)/4)) (√((361)/4)) =((19)/2) ^3 (√(−((35)/2)−((19)/2))) +^3 (√(((−35)/2)+((19)/2))) ^3 (√(−27))+^3 (√(−8)) −5 is solution

$$\sqrt{\left(\frac{\mathrm{35}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(−\mathrm{6}\right)^{\mathrm{3}} } \\ $$$$\sqrt{\frac{\mathrm{1225}}{\mathrm{4}}−\mathrm{216}} \\ $$$$\sqrt{\frac{\mathrm{1225}−\mathrm{864}}{\mathrm{4}}} \\ $$$$\sqrt{\frac{\mathrm{361}}{\mathrm{4}}}\:=\frac{\mathrm{19}}{\mathrm{2}} \\ $$$$\:^{\mathrm{3}} \sqrt{−\frac{\mathrm{35}}{\mathrm{2}}−\frac{\mathrm{19}}{\mathrm{2}}}\:+\:^{\mathrm{3}} \sqrt{\frac{−\mathrm{35}}{\mathrm{2}}+\frac{\mathrm{19}}{\mathrm{2}}} \\ $$$$\:^{\mathrm{3}} \sqrt{−\mathrm{27}}+\:^{\mathrm{3}} \sqrt{−\mathrm{8}} \\ $$$$−\mathrm{5}\:{is}\:{solution} \\ $$$$ \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply