Question Number 184095 by Shrinava last updated on 02/Jan/23

Answered by mr W last updated on 03/Jan/23

Commented by mr W last updated on 03/Jan/23
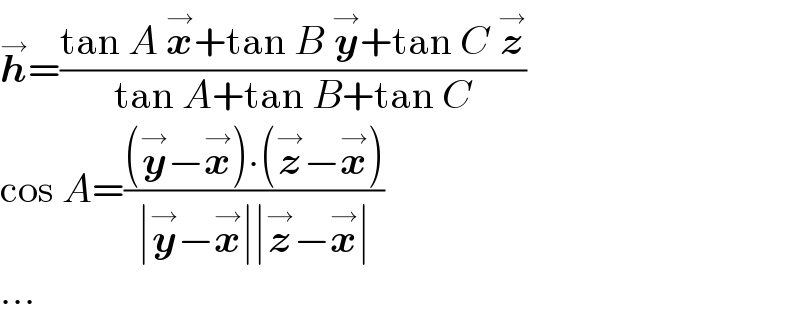
$$\overset{\rightarrow} {\boldsymbol{{h}}}=\frac{\mathrm{tan}\:{A}\:\overset{\rightarrow} {\boldsymbol{{x}}}+\mathrm{tan}\:{B}\:\overset{\rightarrow} {\boldsymbol{{y}}}+\mathrm{tan}\:{C}\:\overset{\rightarrow} {\boldsymbol{{z}}}}{\mathrm{tan}\:{A}+\mathrm{tan}\:{B}+\mathrm{tan}\:{C}} \\ $$$$\mathrm{cos}\:{A}=\frac{\left(\overset{\rightarrow} {\boldsymbol{{y}}}−\overset{\rightarrow} {\boldsymbol{{x}}}\right)\centerdot\left(\overset{\rightarrow} {\boldsymbol{{z}}}−\overset{\rightarrow} {\boldsymbol{{x}}}\right)}{\mid\overset{\rightarrow} {\boldsymbol{{y}}}−\overset{\rightarrow} {\boldsymbol{{x}}}\mid\mid\overset{\rightarrow} {\boldsymbol{{z}}}−\overset{\rightarrow} {\boldsymbol{{x}}}\mid} \\ $$$$… \\ $$
Commented by Shrinava last updated on 03/Jan/23
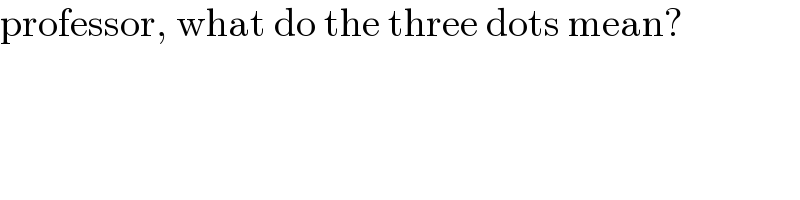
$$\mathrm{professor},\:\mathrm{what}\:\mathrm{do}\:\mathrm{the}\:\mathrm{three}\:\mathrm{dots}\:\mathrm{mean}? \\ $$
Commented by mr W last updated on 03/Jan/23
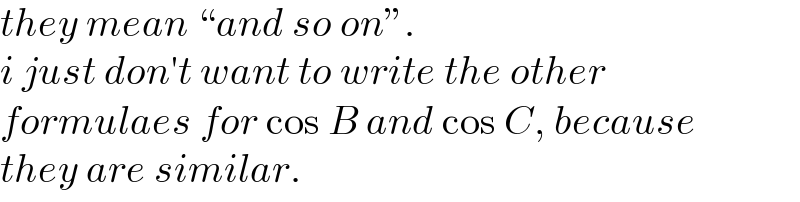
$${they}\:{mean}\:“{and}\:{so}\:{on}''. \\ $$$${i}\:{just}\:{don}'{t}\:{want}\:{to}\:{write}\:{the}\:{other} \\ $$$${formulaes}\:{for}\:\mathrm{cos}\:{B}\:{and}\:\mathrm{cos}\:{C},\:{because} \\ $$$${they}\:{are}\:{similar}. \\ $$
Commented by Shrinava last updated on 03/Jan/23
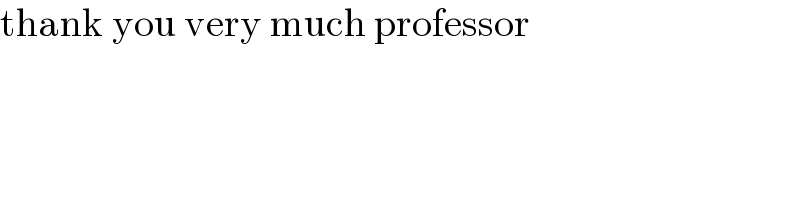
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{professor} \\ $$
Answered by mr W last updated on 03/Jan/23
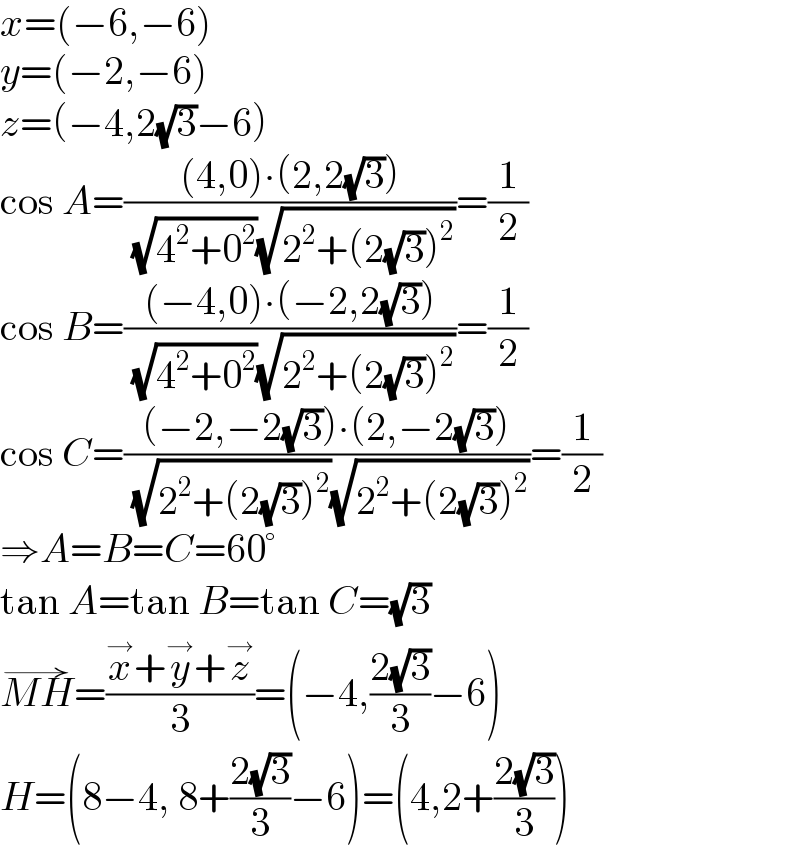
$${x}=\left(−\mathrm{6},−\mathrm{6}\right) \\ $$$${y}=\left(−\mathrm{2},−\mathrm{6}\right) \\ $$$${z}=\left(−\mathrm{4},\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{6}\right) \\ $$$$\mathrm{cos}\:{A}=\frac{\left(\mathrm{4},\mathrm{0}\right)\centerdot\left(\mathrm{2},\mathrm{2}\sqrt{\mathrm{3}}\right)}{\:\sqrt{\mathrm{4}^{\mathrm{2}} +\mathrm{0}^{\mathrm{2}} }\sqrt{\mathrm{2}^{\mathrm{2}} +\left(\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:{B}=\frac{\left(−\mathrm{4},\mathrm{0}\right)\centerdot\left(−\mathrm{2},\mathrm{2}\sqrt{\mathrm{3}}\right)}{\:\sqrt{\mathrm{4}^{\mathrm{2}} +\mathrm{0}^{\mathrm{2}} }\sqrt{\mathrm{2}^{\mathrm{2}} +\left(\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:{C}=\frac{\left(−\mathrm{2},−\mathrm{2}\sqrt{\mathrm{3}}\right)\centerdot\left(\mathrm{2},−\mathrm{2}\sqrt{\mathrm{3}}\right)}{\:\sqrt{\mathrm{2}^{\mathrm{2}} +\left(\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\sqrt{\mathrm{2}^{\mathrm{2}} +\left(\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{A}={B}={C}=\mathrm{60}° \\ $$$$\mathrm{tan}\:{A}=\mathrm{tan}\:{B}=\mathrm{tan}\:{C}=\sqrt{\mathrm{3}} \\ $$$$\overset{\rightarrow} {{MH}}=\frac{\overset{\rightarrow} {{x}}+\overset{\rightarrow} {{y}}+\overset{\rightarrow} {{z}}}{\mathrm{3}}=\left(−\mathrm{4},\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}−\mathrm{6}\right) \\ $$$${H}=\left(\mathrm{8}−\mathrm{4},\:\mathrm{8}+\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}−\mathrm{6}\right)=\left(\mathrm{4},\mathrm{2}+\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\right) \\ $$
Commented by Shrinava last updated on 03/Jan/23
$$\mathrm{perfect}\:\mathrm{professor},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
