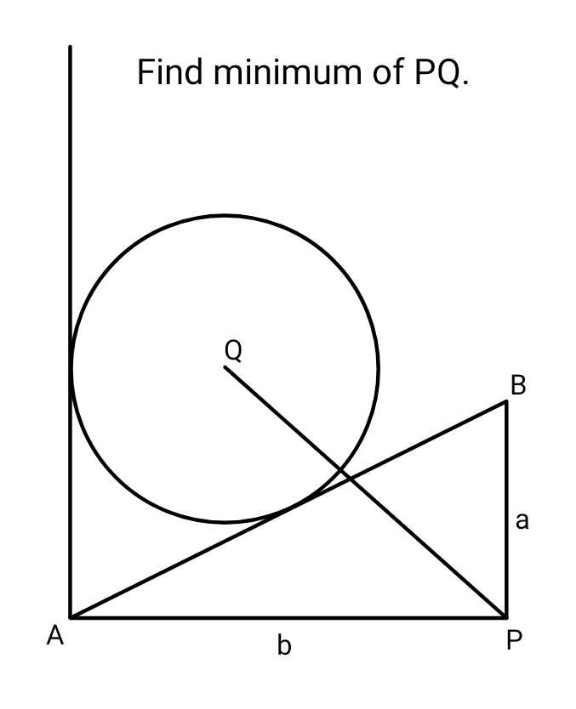
Question Number 184135 by ajfour last updated on 03/Jan/23
Commented by mr W last updated on 03/Jan/23

$${PQ}_{{min}} ={b}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{{a}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right)} \\ $$
Answered by ajfour last updated on 03/Jan/23

Commented by ajfour last updated on 03/Jan/23
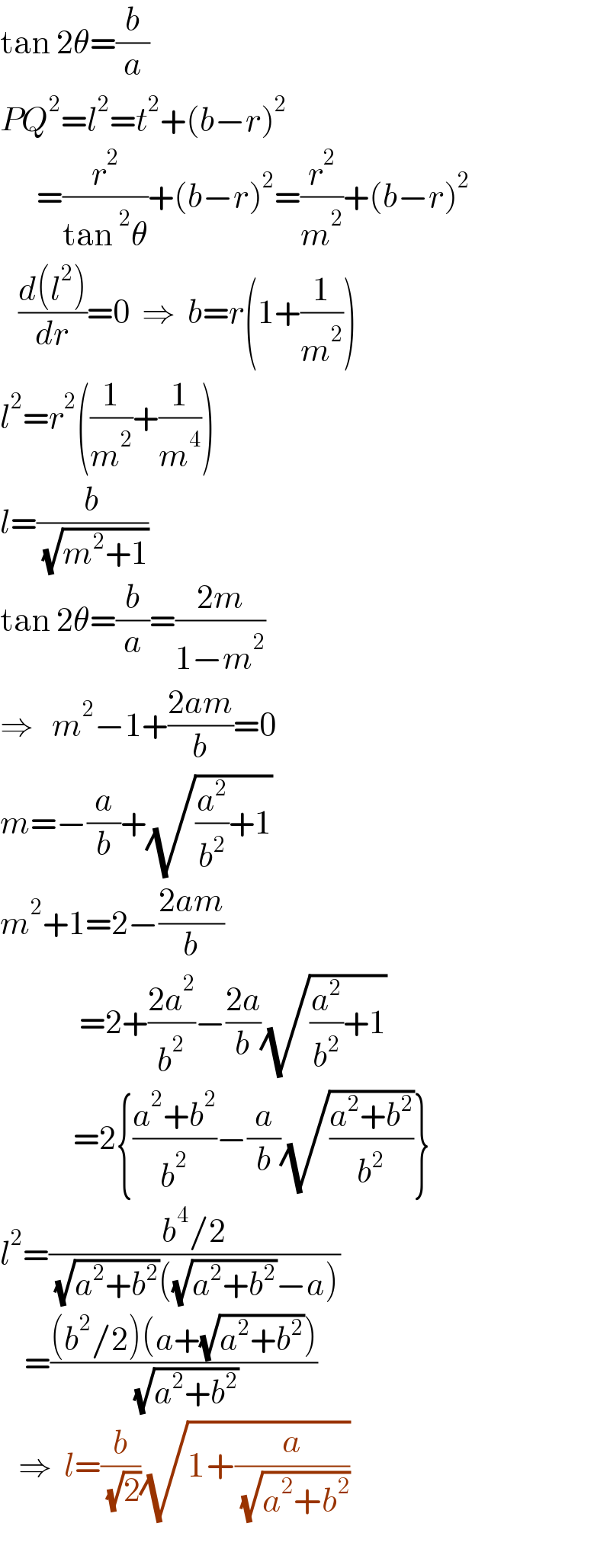
$$\mathrm{tan}\:\mathrm{2}\theta=\frac{{b}}{{a}} \\ $$$${PQ}^{\mathrm{2}} ={l}^{\mathrm{2}} ={t}^{\mathrm{2}} +\left({b}−{r}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\frac{{r}^{\mathrm{2}} }{\mathrm{tan}\:^{\mathrm{2}} \theta}+\left({b}−{r}\right)^{\mathrm{2}} =\frac{{r}^{\mathrm{2}} }{{m}^{\mathrm{2}} }+\left({b}−{r}\right)^{\mathrm{2}} \\ $$$$\:\:\:\frac{{d}\left({l}^{\mathrm{2}} \right)}{{dr}}=\mathrm{0}\:\:\Rightarrow\:\:{b}={r}\left(\mathrm{1}+\frac{\mathrm{1}}{{m}^{\mathrm{2}} }\right) \\ $$$${l}^{\mathrm{2}} ={r}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{m}^{\mathrm{2}} }+\frac{\mathrm{1}}{{m}^{\mathrm{4}} }\right) \\ $$$${l}=\frac{{b}}{\:\sqrt{{m}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathrm{tan}\:\mathrm{2}\theta=\frac{{b}}{{a}}=\frac{\mathrm{2}{m}}{\mathrm{1}−{m}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\:{m}^{\mathrm{2}} −\mathrm{1}+\frac{\mathrm{2}{am}}{{b}}=\mathrm{0} \\ $$$${m}=−\frac{{a}}{{b}}+\sqrt{\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }+\mathrm{1}} \\ $$$${m}^{\mathrm{2}} +\mathrm{1}=\mathrm{2}−\frac{\mathrm{2}{am}}{{b}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}+\frac{\mathrm{2}{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\frac{\mathrm{2}{a}}{{b}}\sqrt{\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left\{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\frac{{a}}{{b}}\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} }}\right\} \\ $$$${l}^{\mathrm{2}} =\frac{{b}^{\mathrm{4}} /\mathrm{2}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\left(\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }−{a}\right)} \\ $$$$\:\:\:\:=\frac{\left({b}^{\mathrm{2}} /\mathrm{2}\right)\left({a}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$$\:\:\:\Rightarrow\:\:{l}=\frac{{b}}{\:\sqrt{\mathrm{2}}}\sqrt{\mathrm{1}+\frac{{a}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}} \\ $$$$ \\ $$
Commented by ajfour last updated on 03/Jan/23

$${yes}\:{sir},\:{thanks}. \\ $$
Commented by mr W last updated on 03/Jan/23
$${very}\:{nice}\:{question}\:{and}\:{solution}! \\ $$
Answered by mr W last updated on 03/Jan/23

Commented by mr W last updated on 04/Jan/23

$$\boldsymbol{{an}}\:\boldsymbol{{other}}\:\boldsymbol{{approach}} \\ $$$${locus}\:{of}\:{Q}\:{is}\:{bisector}\:{of}\:{angle}\:\angle{NAB}. \\ $$$${the}\:{minimum}\:{of}\:{PQ}\:{is}\:{the}\:{distance} \\ $$$${from}\:{P}\:{to}\:{this}\:{bisector}:\:{PQ}'. \\ $$$$\theta=\frac{\beta}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\beta=\frac{{a}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{cos}\:\frac{\beta}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:\beta+\mathrm{1}\right)}\:=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{{a}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right)} \\ $$$$\Rightarrow{PQ}'={b}\:\mathrm{cos}\:\theta={b}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:={b}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{{a}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right)}={PQ}_{{min}} \\ $$
Commented by ajfour last updated on 04/Jan/23
$${this}\:{is}\:{best}\:{approach},\:{thanks}\:{sir}. \\ $$
