Question Number 184304 by mathlove last updated on 05/Jan/23
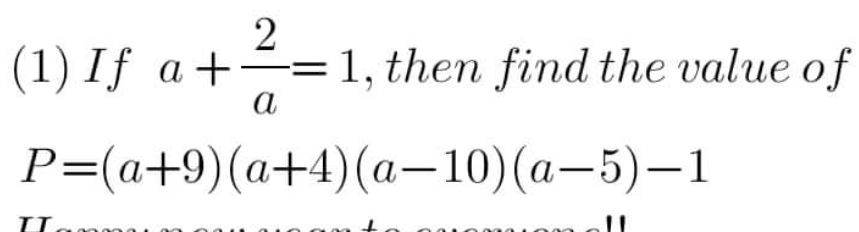
Answered by Frix last updated on 05/Jan/23

$${a}=\frac{\mathrm{1}+\sqrt{\mathrm{4}{t}+\mathrm{221}}}{\mathrm{2}} \\ $$$${a}+\frac{\mathrm{2}}{{a}}=\mathrm{1}\:\Leftrightarrow\:{a}^{\mathrm{2}} −{a}+\mathrm{2}=\mathrm{0}\:\Leftrightarrow\:{t}=−\mathrm{57} \\ $$$${P}={t}^{\mathrm{2}} −\mathrm{1226}=\mathrm{2023} \\ $$
Answered by Rasheed.Sindhi last updated on 05/Jan/23
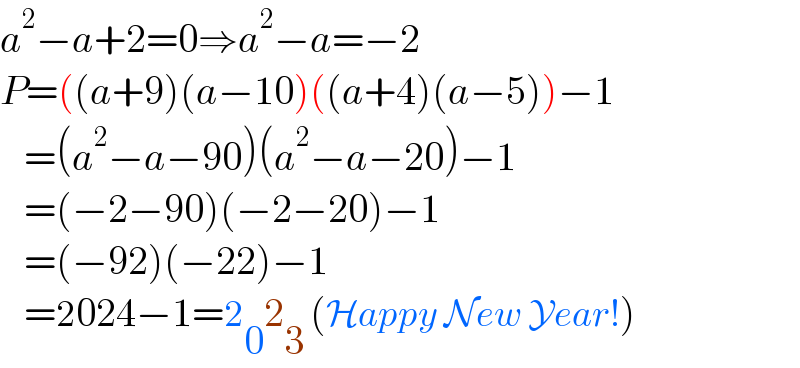
$${a}^{\mathrm{2}} −{a}+\mathrm{2}=\mathrm{0}\Rightarrow{a}^{\mathrm{2}} −{a}=−\mathrm{2} \\ $$$${P}=\left(\left({a}+\mathrm{9}\right)\left({a}−\mathrm{10}\right)\left(\left({a}+\mathrm{4}\right)\left({a}−\mathrm{5}\right)\right)−\mathrm{1}\right. \\ $$$$\:\:\:=\left({a}^{\mathrm{2}} −{a}−\mathrm{90}\right)\left({a}^{\mathrm{2}} −{a}−\mathrm{20}\right)−\mathrm{1} \\ $$$$\:\:\:=\left(−\mathrm{2}−\mathrm{90}\right)\left(−\mathrm{2}−\mathrm{20}\right)−\mathrm{1} \\ $$$$\:\:\:=\left(−\mathrm{92}\right)\left(−\mathrm{22}\right)−\mathrm{1} \\ $$$$\:\:\:=\mathrm{2024}−\mathrm{1}=\mathrm{2}_{\mathrm{0}} \mathrm{2}_{\mathrm{3}} \:\left(\mathcal{H}{appy}\:\mathcal{N}{ew}\:\mathcal{Y}{ear}!\right) \\ $$
Commented by Frix last updated on 05/Jan/23
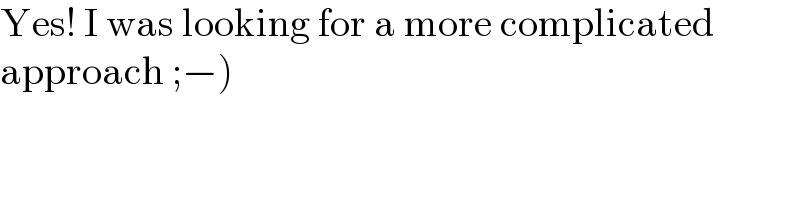
$$\mathrm{Yes}!\:\mathrm{I}\:\mathrm{was}\:\mathrm{looking}\:\mathrm{for}\:\mathrm{a}\:\mathrm{more}\:\mathrm{complicated} \\ $$$$\left.\mathrm{approach}\:;−\right) \\ $$
Commented by Rasheed.Sindhi last updated on 05/Jan/23

$$\mathcal{E}{xcuse}\:{me}\:{sir},\:\left(\mathrm{1}\right)\:{Your}\:{approach} \\ $$$${is}\:{complicated}.\left(\mathrm{2}\right){Yet}\:{your}\:{answer} \\ $$$$\left.{is}\:{too}\:{short}\:{to}\:{understand}\::\right) \\ $$$${Or}\: \\ $$$${I}'{m}\:{not}\:{sharp}\:{enough}… \\ $$
