Question Number 184398 by HeferH last updated on 06/Jan/23
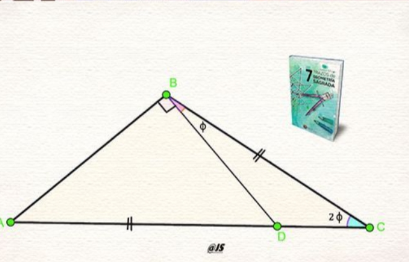
Answered by som(math1967) last updated on 06/Jan/23
![((BD)/(BC))=((sin2φ)/(sin(180−3φ)))=((sin2φ)/(sin3φ)) ((AD)/(BD))=((sin90)/(sin(90−3φ)))=(1/(cos3φ)) BD=ADcos3φ ((ADcos3φ)/(AD))=((sin2φ)/(sin3φ)) [∵BC=AD] sin3φcos3φ=sin2φ 2sin3φcos3φ=2sin2φ sin6φ=2sin2φ 3sin2φ−4sin^3 2φ=2sin2φ ⇒3−4sin^2 2φ=2 [φ≠0] sin2φ=(1/2) 2φ=30⇒φ=15](https://www.tinkutara.com/question/Q184400.png)
$$\:\frac{{BD}}{{BC}}=\frac{{sin}\mathrm{2}\phi}{{sin}\left(\mathrm{180}−\mathrm{3}\phi\right)}=\frac{{sin}\mathrm{2}\phi}{{sin}\mathrm{3}\phi} \\ $$$$\frac{{AD}}{{BD}}=\frac{{sin}\mathrm{90}}{{sin}\left(\mathrm{90}−\mathrm{3}\phi\right)}=\frac{\mathrm{1}}{{cos}\mathrm{3}\phi} \\ $$$$\:{BD}={ADcos}\mathrm{3}\phi \\ $$$$\:\frac{{ADcos}\mathrm{3}\phi}{{AD}}=\frac{{sin}\mathrm{2}\phi}{{sin}\mathrm{3}\phi}\:\:\:\left[\because{BC}={AD}\right] \\ $$$${sin}\mathrm{3}\phi{cos}\mathrm{3}\phi={sin}\mathrm{2}\phi \\ $$$$\mathrm{2}{sin}\mathrm{3}\phi{cos}\mathrm{3}\phi=\mathrm{2}{sin}\mathrm{2}\phi \\ $$$${sin}\mathrm{6}\phi=\mathrm{2}{sin}\mathrm{2}\phi \\ $$$$\mathrm{3}{sin}\mathrm{2}\phi−\mathrm{4}{sin}^{\mathrm{3}} \mathrm{2}\phi=\mathrm{2}{sin}\mathrm{2}\phi \\ $$$$\Rightarrow\mathrm{3}−\mathrm{4}{sin}^{\mathrm{2}} \mathrm{2}\phi=\mathrm{2}\:\:\:\left[\phi\neq\mathrm{0}\right] \\ $$$$\:{sin}\mathrm{2}\phi=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\mathrm{2}\phi=\mathrm{30}\Rightarrow\phi=\mathrm{15} \\ $$
