Question-184441

Question Number 184441 by ajfour last updated on 06/Jan/23

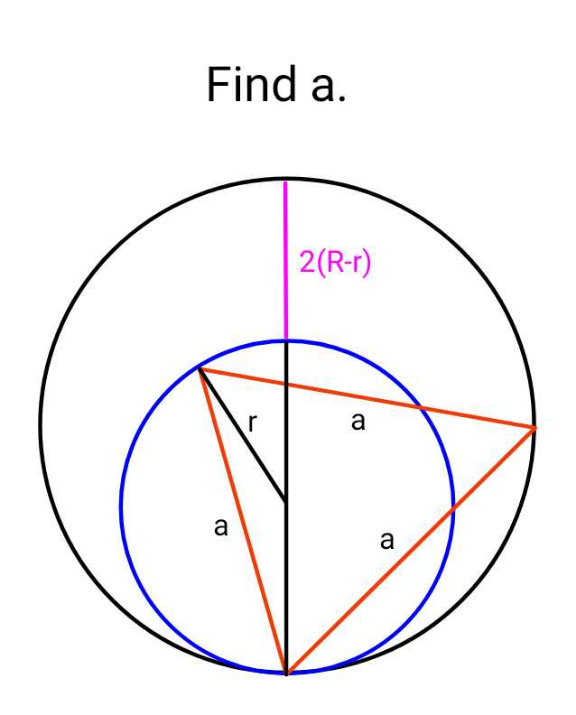
Commented by mr W last updated on 07/Jan/23

$${a}=\frac{\sqrt{\mathrm{3}}{Rr}}{\:\sqrt{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} −{Rr}}} \\ $$

Answered by ajfour last updated on 07/Jan/23

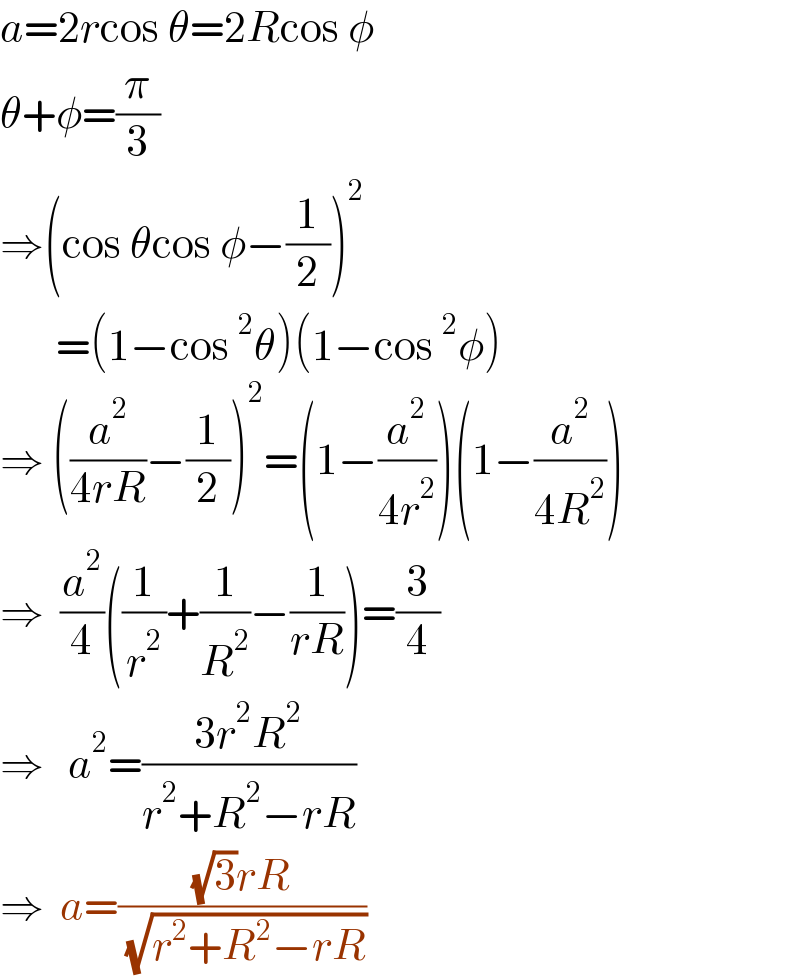
a=2rcos θ=2Rcos φ θ+φ=(π/3) ⇒(cos θcos φ−(1/2))^2 =(1−cos^2 θ)(1−cos^2 φ) ⇒ ((a^2 /(4rR))−(1/2))^2 =(1−(a^2 /(4r^2 )))(1−(a^2 /(4R^2 ))) ⇒ (a^2 /4)((1/r^2 )+(1/R^2 )−(1/(rR)))=(3/4) ⇒ a^2 =((3r^2 R^2 )/(r^2 +R^2 −rR)) ⇒ a=(((√3)rR)/( (√(r^2 +R^2 −rR))))

$${a}=\mathrm{2}{r}\mathrm{cos}\:\theta=\mathrm{2}{R}\mathrm{cos}\:\phi \\ $$$$\theta+\phi=\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow\left(\mathrm{cos}\:\theta\mathrm{cos}\:\phi−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \theta\right)\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \phi\right) \\ $$$$\Rightarrow\:\left(\frac{{a}^{\mathrm{2}} }{\mathrm{4}{rR}}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}{r}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}{R}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\:\:\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\left(\frac{\mathrm{1}}{{r}^{\mathrm{2}} }+\frac{\mathrm{1}}{{R}^{\mathrm{2}} }−\frac{\mathrm{1}}{{rR}}\right)=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\:\:\:{a}^{\mathrm{2}} =\frac{\mathrm{3}{r}^{\mathrm{2}} {R}^{\mathrm{2}} }{{r}^{\mathrm{2}} +{R}^{\mathrm{2}} −{rR}} \\ $$$$\Rightarrow\:\:{a}=\frac{\sqrt{\mathrm{3}}{rR}}{\:\sqrt{{r}^{\mathrm{2}} +{R}^{\mathrm{2}} −{rR}}} \\ $$

Commented by mr W last updated on 07/Jan/23

��

Answered by mr W last updated on 07/Jan/23

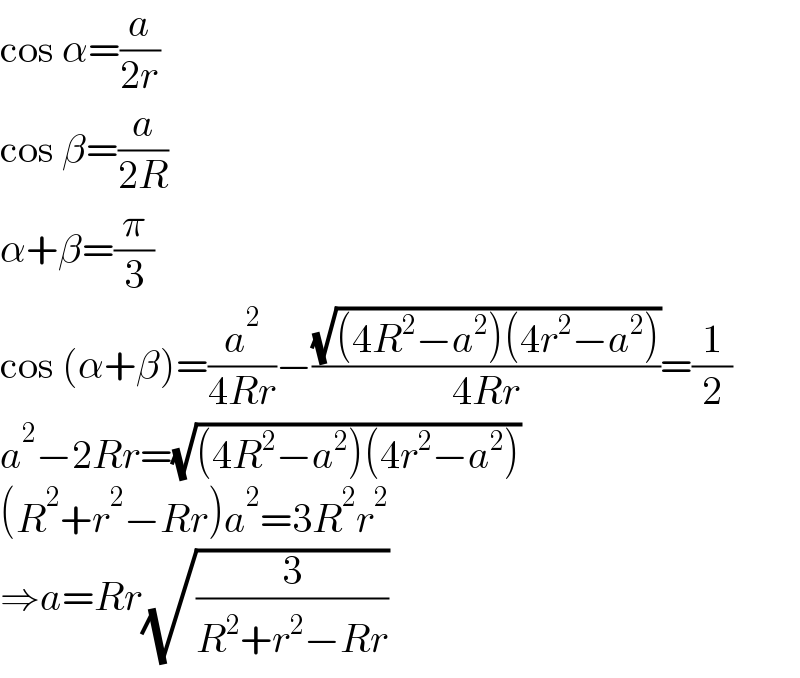
cos α=(a/(2r)) cos β=(a/(2R)) α+β=(π/3) cos (α+β)=(a^2 /(4Rr))−((√((4R^2 −a^2 )(4r^2 −a^2 )))/(4Rr))=(1/2) a^2 −2Rr=(√((4R^2 −a^2 )(4r^2 −a^2 ))) (R^2 +r^2 −Rr)a^2 =3R^2 r^2 ⇒a=Rr(√(3/(R^2 +r^2 −Rr)))

$$\mathrm{cos}\:\alpha=\frac{{a}}{\mathrm{2}{r}} \\ $$$$\mathrm{cos}\:\beta=\frac{{a}}{\mathrm{2}{R}} \\ $$$$\alpha+\beta=\frac{\pi}{\mathrm{3}} \\ $$$$\mathrm{cos}\:\left(\alpha+\beta\right)=\frac{{a}^{\mathrm{2}} }{\mathrm{4}{Rr}}−\frac{\sqrt{\left(\mathrm{4}{R}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\left(\mathrm{4}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}}{\mathrm{4}{Rr}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} −\mathrm{2}{Rr}=\sqrt{\left(\mathrm{4}{R}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\left(\mathrm{4}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)} \\ $$$$\left({R}^{\mathrm{2}} +{r}^{\mathrm{2}} −{Rr}\right){a}^{\mathrm{2}} =\mathrm{3}{R}^{\mathrm{2}} {r}^{\mathrm{2}} \\ $$$$\Rightarrow{a}={Rr}\sqrt{\frac{\mathrm{3}}{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} −{Rr}}} \\ $$

Commented by mr W last updated on 07/Jan/23