Menu Close

Question-184478

Tinku Tara 0 Comments
Pin




Question Number 184478 by Shrinava last updated on 07/Jan/23
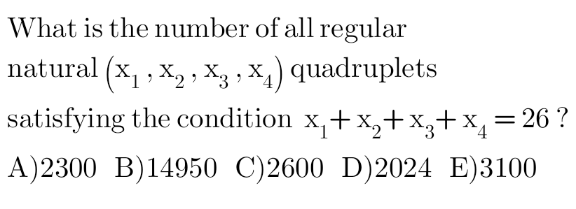
Answered by mr W last updated on 08/Jan/23
“generating function” method (x+x^2 +x^3 +...)^4 =(x^4 /((1−x)^4 ))=x^4 Σ_(k=0) ^∞ C_3 ^(k+3) x^k 4+k=26 ⇒k=22 C_3 ^(22+3) =((25×24×23)/6)=2300 ✓ or using “bars & stars” method: C_(r−1) ^(n−1) =C_(4−1) ^(26−1) =C_3 ^(25) =2300 ✓
$$“\boldsymbol{{generating}}\:\boldsymbol{{function}}''\:\boldsymbol{{method}} \\ $$$$\left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…\right)^{\mathrm{4}} =\frac{{x}^{\mathrm{4}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }={x}^{\mathrm{4}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{3}} ^{{k}+\mathrm{3}} {x}^{{k}} \\ $$$$\mathrm{4}+{k}=\mathrm{26}\:\Rightarrow{k}=\mathrm{22} \\ $$$${C}_{\mathrm{3}} ^{\mathrm{22}+\mathrm{3}} =\frac{\mathrm{25}×\mathrm{24}×\mathrm{23}}{\mathrm{6}}=\mathrm{2300}\:\checkmark \\ $$$$ \\ $$$${or}\:{using}\:“\boldsymbol{{bars}}\:\&\:\boldsymbol{{stars}}''\:{method}: \\ $$$${C}_{{r}−\mathrm{1}} ^{{n}−\mathrm{1}} ={C}_{\mathrm{4}−\mathrm{1}} ^{\mathrm{26}−\mathrm{1}} ={C}_{\mathrm{3}} ^{\mathrm{25}} =\mathrm{2300}\:\checkmark \\ $$
Commented by Shrinava last updated on 07/Jan/23
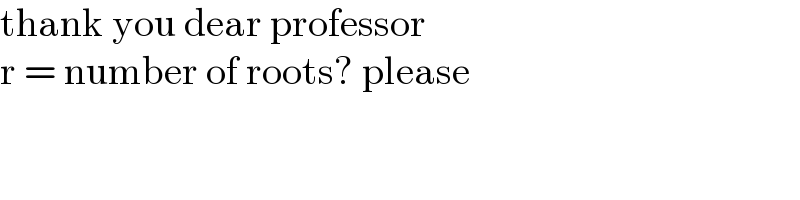
thank you dear professor r = number of roots? please
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor} \\ $$$$\mathrm{r}\:=\:\mathrm{number}\:\mathrm{of}\:\mathrm{roots}?\:\mathrm{please} \\ $$
Commented by mr W last updated on 07/Jan/23
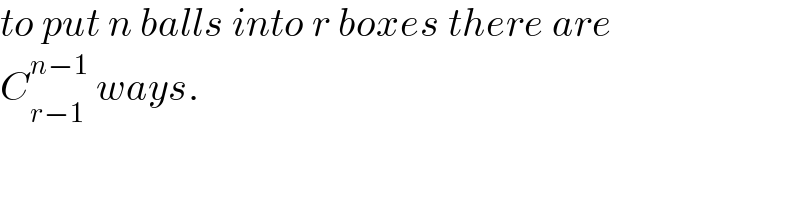
to put n balls into r boxes there are C_(r−1) ^(n−1) ways.
$${to}\:{put}\:{n}\:{balls}\:{into}\:{r}\:{boxes}\:{there}\:{are} \\ $$$${C}_{{r}−\mathrm{1}} ^{{n}−\mathrm{1}} \:{ways}. \\ $$
Commented by Shrinava last updated on 07/Jan/23
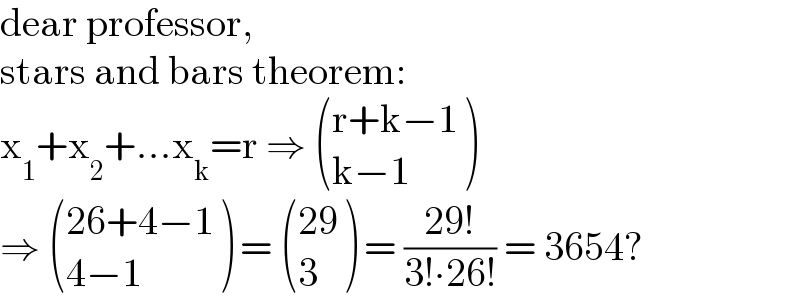
dear professor, stars and bars theorem: x_1 +x_2 +...x_k =r ⇒ (((r+k−1)),((k−1)) ) ⇒ (((26+4−1)),((4−1)) ) = (((29)),(3) ) = ((29!)/(3!∙26!)) = 3654?
$$\mathrm{dear}\:\mathrm{professor}, \\ $$$$\mathrm{stars}\:\mathrm{and}\:\mathrm{bars}\:\mathrm{theorem}: \\ $$$$\mathrm{x}_{\mathrm{1}} +\mathrm{x}_{\mathrm{2}} +…\mathrm{x}_{\mathrm{k}} =\mathrm{r}\:\Rightarrow\:\begin{pmatrix}{\mathrm{r}+\mathrm{k}−\mathrm{1}}\\{\mathrm{k}−\mathrm{1}}\end{pmatrix} \\ $$$$\Rightarrow\:\begin{pmatrix}{\mathrm{26}+\mathrm{4}−\mathrm{1}}\\{\mathrm{4}−\mathrm{1}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{29}}\\{\mathrm{3}}\end{pmatrix}\:=\:\frac{\mathrm{29}!}{\mathrm{3}!\centerdot\mathrm{26}!}\:=\:\mathrm{3654}? \\ $$
Commented by mr W last updated on 08/Jan/23
example: x_1 +x_2 +x_3 =8 x_i ≥1 it means in how many ways can 8 apples be distributed to 3 persons such that each person gets at least one apple? in following a star ★ means an apple. to distribute 8 apples into 3 portions we just need to separate the 8 stars with 2 bars, like this: ★∣★★★★★∣★★ we see there are 7 positions where we can place the 2 bars, therefore there are C_2 ^7 ways to distribute 8 apples to 3 persons. generally there are C_(r−1) ^(n−1) ways to distribute n identical objects into r different boxes such that each box gets at least one object. this method is called “stars & bars” method. so x_1 +x_2 +...x_r =n with x_i ∈N has C_(r−1) ^(n−1) = (((n−1)),((r−1)) ) solutions.
$${example}: \\ $$$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} =\mathrm{8} \\ $$$${x}_{{i}} \geqslant\mathrm{1} \\ $$$${it}\:{means}\:{in}\:{how}\:{many}\:{ways}\:{can}\:\mathrm{8} \\ $$$${apples}\:{be}\:{distributed}\:{to}\:\mathrm{3}\:{persons} \\ $$$${such}\:{that}\:{each}\:{person}\:{gets}\:{at}\:{least} \\ $$$${one}\:{apple}? \\ $$$${in}\:{following}\:{a}\:{star}\:\bigstar\:\:{means}\:{an}\:{apple}. \\ $$$${to}\:{distribute}\:\mathrm{8}\:{apples}\:{into}\:\mathrm{3}\:{portions} \\ $$$${we}\:{just}\:{need}\:{to}\:{separate}\:{the}\:\mathrm{8}\:{stars} \\ $$$${with}\:\mathrm{2}\:{bars},\:{like}\:{this}: \\ $$$$\bigstar\mid\bigstar\bigstar\bigstar\bigstar\bigstar\mid\bigstar\bigstar \\ $$$${we}\:{see}\:{there}\:{are}\:\mathrm{7}\:{positions}\:{where}\:{we} \\ $$$${can}\:{place}\:{the}\:\mathrm{2}\:{bars},\:{therefore}\:{there} \\ $$$${are}\:{C}_{\mathrm{2}} ^{\mathrm{7}} \:{ways}\:{to}\:{distribute}\:\mathrm{8}\:{apples}\:{to} \\ $$$$\mathrm{3}\:{persons}.\:{generally}\:{there}\:{are}\:{C}_{{r}−\mathrm{1}} ^{{n}−\mathrm{1}} \\ $$$${ways}\:{to}\:{distribute}\:{n}\:{identical}\:{objects} \\ $$$${into}\:{r}\:{different}\:{boxes}\:{such}\:{that}\:{each} \\ $$$${box}\:{gets}\:{at}\:{least}\:{one}\:{object}. \\ $$$${this}\:{method}\:{is}\:{called}\:“{stars}\:\&\:{bars}'' \\ $$$${method}. \\ $$$${so}\:{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +…{x}_{{r}} ={n}\:{with}\:{x}_{{i}} \:\in{N} \\ $$$${has}\:{C}_{{r}−\mathrm{1}} ^{{n}−\mathrm{1}} =\begin{pmatrix}{{n}−\mathrm{1}}\\{{r}−\mathrm{1}}\end{pmatrix}\:{solutions}. \\ $$
Commented by mr W last updated on 08/Jan/23
i have used two methods: “generating function” method and “stars & bars” method. the “stars & bars” method is explained above. it′s easy to understand. but you can use it only for solving easy cases. the generating function method is much more powerful, and can solve complicated cases like this: x_1 +x_2 +x_3 +x_4 =26 all numbers are natural numbers, but x_1 are odd, x_2 are even equal or greater than 6, while x_4 are at most 5. the number of solutions under these conditions is the coefficient of term x^(26) in the expansion of following expression: (x+x^3 +x^5 +...)(x^6 +x^8 +x^(10) +...)(x+x^2 +x^3 +...)(x+x^2 +x^3 +x^4 +x^5 ) =(x/(1−x^2 ))×(x^6 /(1−x^2 ))×(x/(1−x))×((x(1−x^5 ))/(1−x)) =((x^9 (1−x^5 ))/((1−x)^2 (1−x^2 )^2 )) the coefficient of x^(26) is 190. that means there are 190 solutions.
$${i}\:{have}\:{used}\:{two}\:{methods}: \\ $$$$“{generating}\:{function}''\:{method}\:{and} \\ $$$$“{stars}\:\&\:{bars}''\:{method}.\: \\ $$$${the}\:“{stars}\:\&\:{bars}''\:{method}\:{is}\: \\ $$$${explained}\:{above}.\:{it}'{s}\:{easy}\:{to}\: \\ $$$${understand}.\:{but}\:{you}\:{can}\:{use} \\ $$$${it}\:{only}\:{for}\:{solving}\:{easy}\:{cases}.\: \\ $$$${the}\:{generating}\:{function}\:{method}\:{is}\: \\ $$$${much}\:{more}\:{powerful},\:{and}\:{can}\:{solve}\: \\ $$$${complicated}\:{cases}\:{like}\:{this}: \\ $$$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +{x}_{\mathrm{4}} =\mathrm{26} \\ $$$${all}\:{numbers}\:{are}\:{natural}\:{numbers}, \\ $$$${but}\:{x}_{\mathrm{1}} \:{are}\:{odd},\:{x}_{\mathrm{2}} \:{are}\:{even}\:{equal}\:{or} \\ $$$${greater}\:{than}\:\mathrm{6},\:{while}\:{x}_{\mathrm{4}} \:{are}\:{at}\:{most}\:\mathrm{5}. \\ $$$${the}\:{number}\:{of}\:{solutions}\:{under}\:{these} \\ $$$${conditions}\:{is}\:{the}\:{coefficient}\:{of}\:{term} \\ $$$${x}^{\mathrm{26}} \:{in}\:{the}\:{expansion}\:{of}\:{following} \\ $$$${expression}: \\ $$$$\left({x}+{x}^{\mathrm{3}} +{x}^{\mathrm{5}} +…\right)\left({x}^{\mathrm{6}} +{x}^{\mathrm{8}} +{x}^{\mathrm{10}} +…\right)\left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…\right)\left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +{x}^{\mathrm{5}} \right) \\ $$$$=\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }×\frac{{x}^{\mathrm{6}} }{\mathrm{1}−{x}^{\mathrm{2}} }×\frac{{x}}{\mathrm{1}−{x}}×\frac{{x}\left(\mathrm{1}−{x}^{\mathrm{5}} \right)}{\mathrm{1}−{x}} \\ $$$$=\frac{{x}^{\mathrm{9}} \left(\mathrm{1}−{x}^{\mathrm{5}} \right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${the}\:{coefficient}\:{of}\:{x}^{\mathrm{26}} \:{is}\:\mathrm{190}.\:{that} \\ $$$${means}\:{there}\:{are}\:\mathrm{190}\:{solutions}.\: \\ $$
Commented by Shrinava last updated on 08/Jan/23
cool dear professor thank you
$$\mathrm{cool}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *