Question Number 184514 by BOYQOBILOV last updated on 08/Jan/23

Answered by SEKRET last updated on 19/Jan/23
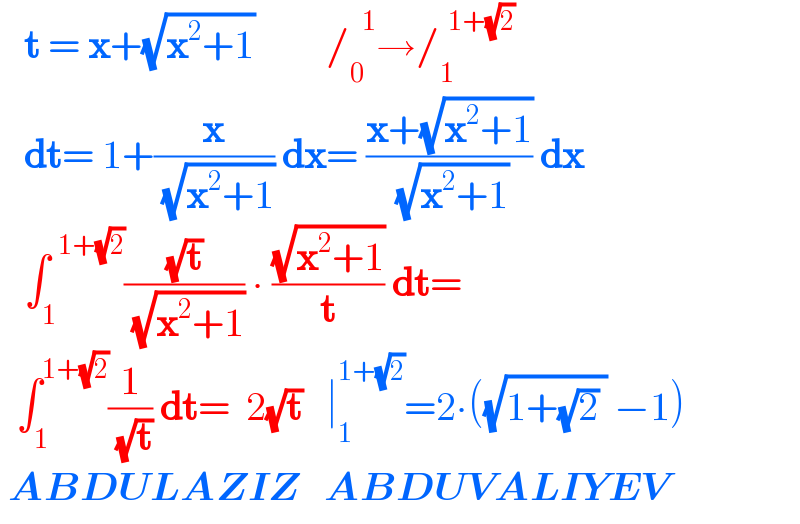
$$\:\:\:\boldsymbol{\mathrm{t}}\:=\:\boldsymbol{\mathrm{x}}+\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}\:\:\:\:\:\:\:\:\:/_{\mathrm{0}} ^{\:\:\:\mathrm{1}} \rightarrow/_{\mathrm{1}} ^{\:\:\mathrm{1}+\sqrt{\mathrm{2}}} \\ $$$$\:\:\:\boldsymbol{\mathrm{dt}}=\:\mathrm{1}+\frac{\boldsymbol{\mathrm{x}}}{\:\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}}\:\boldsymbol{\mathrm{dx}}=\:\frac{\boldsymbol{\mathrm{x}}+\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}}{\:\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}}\:\boldsymbol{\mathrm{dx}} \\ $$$$\:\:\:\int_{\mathrm{1}} ^{\:\:\mathrm{1}+\sqrt{\mathrm{2}}} \frac{\sqrt{\boldsymbol{\mathrm{t}}}}{\:\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}}\:\centerdot\:\frac{\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}}{\boldsymbol{\mathrm{t}}}\:\boldsymbol{\mathrm{dt}}= \\ $$$$\:\:\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \frac{\mathrm{1}}{\:\sqrt{\boldsymbol{\mathrm{t}}}}\:\boldsymbol{\mathrm{dt}}=\:\:\mathrm{2}\sqrt{\boldsymbol{\mathrm{t}}}\:\:\:\mid_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} =\mathrm{2}\centerdot\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{2}}\:}\:−\mathrm{1}\right) \\ $$$$\:\boldsymbol{{ABDULAZIZ}}\:\:\:\boldsymbol{{ABDUVALIYEV}} \\ $$
