Question Number 184523 by cortano1 last updated on 08/Jan/23

Answered by SEKRET last updated on 08/Jan/23
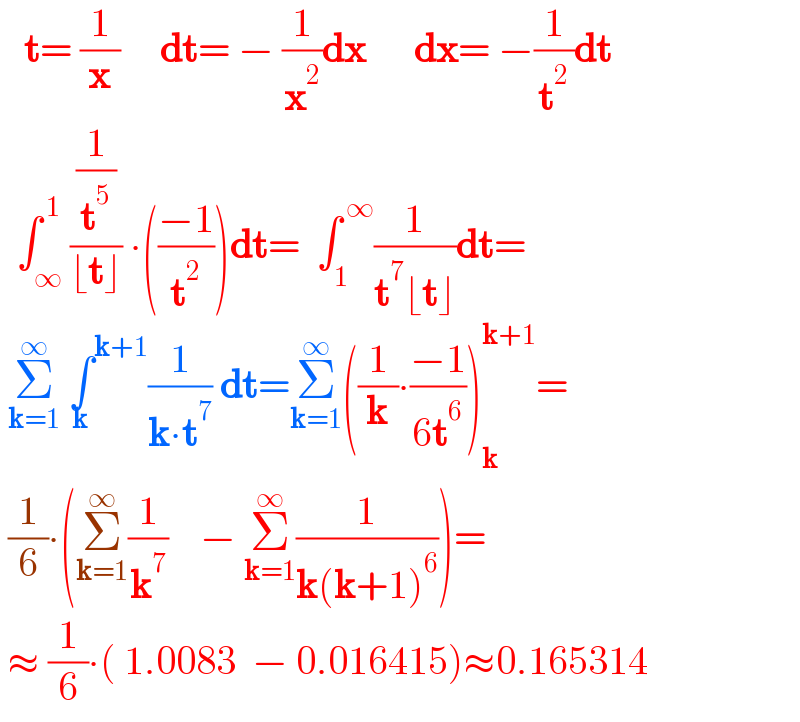
$$\:\:\:\boldsymbol{\mathrm{t}}=\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\:\:\:\:\:\boldsymbol{\mathrm{dt}}=\:−\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }\boldsymbol{\mathrm{dx}}\:\:\:\:\:\:\boldsymbol{\mathrm{dx}}=\:−\frac{\mathrm{1}}{\boldsymbol{\mathrm{t}}^{\mathrm{2}} }\boldsymbol{\mathrm{dt}} \\ $$$$\:\:\int_{\infty} ^{\:\mathrm{1}} \frac{\frac{\mathrm{1}}{\boldsymbol{\mathrm{t}}^{\mathrm{5}} }}{\lfloor\boldsymbol{\mathrm{t}}\rfloor}\:\centerdot\left(\frac{−\mathrm{1}}{\boldsymbol{\mathrm{t}}^{\mathrm{2}} }\right)\boldsymbol{\mathrm{dt}}=\:\:\int_{\mathrm{1}} ^{\:\infty} \frac{\mathrm{1}}{\boldsymbol{\mathrm{t}}^{\mathrm{7}} \lfloor\boldsymbol{\mathrm{t}}\rfloor}\boldsymbol{\mathrm{dt}}= \\ $$$$\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\underset{\boldsymbol{\mathrm{k}}} {\int}^{\boldsymbol{\mathrm{k}}+\mathrm{1}} \frac{\mathrm{1}}{\boldsymbol{\mathrm{k}}\centerdot\boldsymbol{\mathrm{t}}^{\mathrm{7}} }\:\boldsymbol{\mathrm{dt}}=\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\boldsymbol{\mathrm{k}}}\centerdot\frac{−\mathrm{1}}{\mathrm{6}\boldsymbol{\mathrm{t}}^{\mathrm{6}} }\right)_{\boldsymbol{\mathrm{k}}} ^{\boldsymbol{\mathrm{k}}+\mathrm{1}} = \\ $$$$\:\frac{\mathrm{1}}{\mathrm{6}}\centerdot\left(\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{k}}^{\mathrm{7}} }\:\:\:\:−\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{k}}\left(\boldsymbol{\mathrm{k}}+\mathrm{1}\right)^{\mathrm{6}} }\right)= \\ $$$$\:\approx\:\frac{\mathrm{1}}{\mathrm{6}}\centerdot\left(\:\mathrm{1}.\mathrm{0083}\:\:−\:\mathrm{0}.\mathrm{016415}\right)\approx\mathrm{0}.\mathrm{165314} \\ $$
Answered by mr W last updated on 08/Jan/23
![I=∫_0 ^1 (x^5 /(⌊(1/x)⌋))dx=? let x=(1/t) dx=−(dt/t^2 ) I=∫_1 ^∞ (dt/(t^7 ⌊t⌋)) =Σ_(k=1) ^∞ ∫_k ^(k+1) (dt/(t^7 ⌊t⌋)) =Σ_(k=1) ^∞ (1/k)∫_k ^(k+1) (dt/t^7 ) =Σ_(k=1) ^∞ (1/k)[−(1/(6t^6 ))]_k ^(k+1) =(1/6)Σ_(k=1) ^∞ (1/k)[(1/k^6 )−(1/((k+1)^6 ))] =(1/6)Σ_(k=1) ^∞ [(1/k^7 )−(1/(k(k+1)^6 ))] =(1/6)(A−B) A=Σ_(k=1) ^∞ (1/k^7 )=ζ(7) ← Riemann Zeta function ζ(s)=Σ_(n=1) ^∞ (1/n^s ) B=Σ_(k=1) ^∞ (1/(k(k+1)^6 )) =Σ_(k=2) ^∞ (1/((k−1)k^6 )) =Σ_(k=2) ^∞ [(1/((k−1)))−(1/k)−(1/k^2 )−(1/k^3 )−(1/k^4 )−(1/k^5 )−(1/k^6 )] =Σ_(k=2) ^∞ (1/((k−1)))−Σ_(k=2) ^∞ (1/k)−Σ_(k=2) ^∞ ((1/k^2 )+(1/k^3 )+(1/k^4 )+(1/k^5 )+(1/k^6 )) =Σ_(k=1) ^∞ (1/k)−Σ_(k=1) ^∞ (1/k)+1−Σ_(k=1) ^∞ ((1/k^2 )+(1/k^3 )+(1/k^4 )+(1/k^5 )+(1/k^6 ))+5 =−[ζ(2)+ζ(3)+ζ(4)+ζ(5)+ζ(6)]+6 I=(1/6)[ζ(7)+ζ(2)+ζ(3)+ζ(4)+ζ(5)+ζ(6)−6] ⇒I=((ζ(2)+ζ(3)+ζ(4)+ζ(5)+ζ(6)+ζ(7))/6)−1 ≈0.165322382919](https://www.tinkutara.com/question/Q184528.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{5}} }{\lfloor\frac{\mathrm{1}}{{x}}\rfloor}{dx}=? \\ $$$${let}\:{x}=\frac{\mathrm{1}}{{t}} \\ $$$${dx}=−\frac{{dt}}{{t}^{\mathrm{2}} } \\ $$$${I}=\int_{\mathrm{1}} ^{\infty} \frac{{dt}}{{t}^{\mathrm{7}} \lfloor{t}\rfloor} \\ $$$$\:\:=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{{k}} ^{{k}+\mathrm{1}} \frac{{dt}}{{t}^{\mathrm{7}} \lfloor{t}\rfloor} \\ $$$$\:\:=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}}\int_{{k}} ^{{k}+\mathrm{1}} \frac{{dt}}{{t}^{\mathrm{7}} } \\ $$$$\:\:=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}}\left[−\frac{\mathrm{1}}{\mathrm{6}{t}^{\mathrm{6}} }\right]_{{k}} ^{{k}+\mathrm{1}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{6}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}}\left[\frac{\mathrm{1}}{{k}^{\mathrm{6}} }−\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{6}} }\right] \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{6}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{{k}^{\mathrm{7}} }−\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)^{\mathrm{6}} }\right] \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{6}}\left({A}−{B}\right) \\ $$$${A}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{7}} }=\zeta\left(\mathrm{7}\right)\:\:\:\leftarrow\:{Riemann}\:{Zeta}\:{function}\:\zeta\left({s}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{{s}} } \\ $$$${B}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)^{\mathrm{6}} } \\ $$$$\:\:\:=\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({k}−\mathrm{1}\right){k}^{\mathrm{6}} } \\ $$$$\:\:\:=\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{\left({k}−\mathrm{1}\right)}−\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\frac{\mathrm{1}}{{k}^{\mathrm{3}} }−\frac{\mathrm{1}}{{k}^{\mathrm{4}} }−\frac{\mathrm{1}}{{k}^{\mathrm{5}} }−\frac{\mathrm{1}}{{k}^{\mathrm{6}} }\right] \\ $$$$\:\:\:=\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({k}−\mathrm{1}\right)}−\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}}−\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{k}^{\mathrm{2}} }+\frac{\mathrm{1}}{{k}^{\mathrm{3}} }+\frac{\mathrm{1}}{{k}^{\mathrm{4}} }+\frac{\mathrm{1}}{{k}^{\mathrm{5}} }+\frac{\mathrm{1}}{{k}^{\mathrm{6}} }\right) \\ $$$$\:\:\:=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}}−\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}}+\mathrm{1}−\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{k}^{\mathrm{2}} }+\frac{\mathrm{1}}{{k}^{\mathrm{3}} }+\frac{\mathrm{1}}{{k}^{\mathrm{4}} }+\frac{\mathrm{1}}{{k}^{\mathrm{5}} }+\frac{\mathrm{1}}{{k}^{\mathrm{6}} }\right)+\mathrm{5} \\ $$$$\:\:\:=−\left[\zeta\left(\mathrm{2}\right)+\zeta\left(\mathrm{3}\right)+\zeta\left(\mathrm{4}\right)+\zeta\left(\mathrm{5}\right)+\zeta\left(\mathrm{6}\right)\right]+\mathrm{6} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{6}}\left[\zeta\left(\mathrm{7}\right)+\zeta\left(\mathrm{2}\right)+\zeta\left(\mathrm{3}\right)+\zeta\left(\mathrm{4}\right)+\zeta\left(\mathrm{5}\right)+\zeta\left(\mathrm{6}\right)−\mathrm{6}\right] \\ $$$$\Rightarrow{I}=\frac{\zeta\left(\mathrm{2}\right)+\zeta\left(\mathrm{3}\right)+\zeta\left(\mathrm{4}\right)+\zeta\left(\mathrm{5}\right)+\zeta\left(\mathrm{6}\right)+\zeta\left(\mathrm{7}\right)}{\mathrm{6}}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\approx\mathrm{0}.\mathrm{165322382919} \\ $$
