Menu Close

Question-184573

Tinku Tara 0 Comments
Pin




Question Number 184573 by mnjuly1970 last updated on 08/Jan/23
Commented by SEKRET last updated on 08/Jan/23
use an triangle
$$\:\:\:\boldsymbol{\mathrm{use}}\:\boldsymbol{\mathrm{an}}\:\boldsymbol{\mathrm{triangle}} \\ $$
Commented by Frix last updated on 08/Jan/23
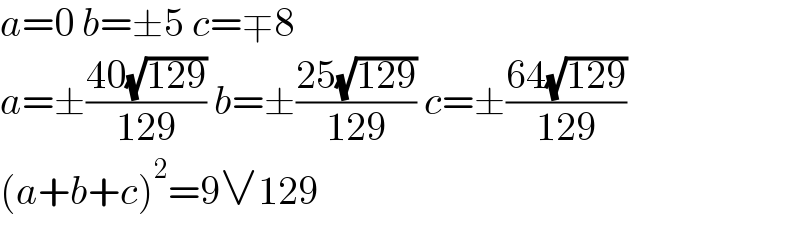
a=0 b=±5 c=∓8 a=±((40(√(129)))/(129)) b=±((25(√(129)))/(129)) c=±((64(√(129)))/(129)) (a+b+c)^2 =9∨129
$${a}=\mathrm{0}\:{b}=\pm\mathrm{5}\:{c}=\mp\mathrm{8} \\ $$$${a}=\pm\frac{\mathrm{40}\sqrt{\mathrm{129}}}{\mathrm{129}}\:{b}=\pm\frac{\mathrm{25}\sqrt{\mathrm{129}}}{\mathrm{129}}\:{c}=\pm\frac{\mathrm{64}\sqrt{\mathrm{129}}}{\mathrm{129}} \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} =\mathrm{9}\vee\mathrm{129} \\ $$
Answered by mr W last updated on 09/Jan/23
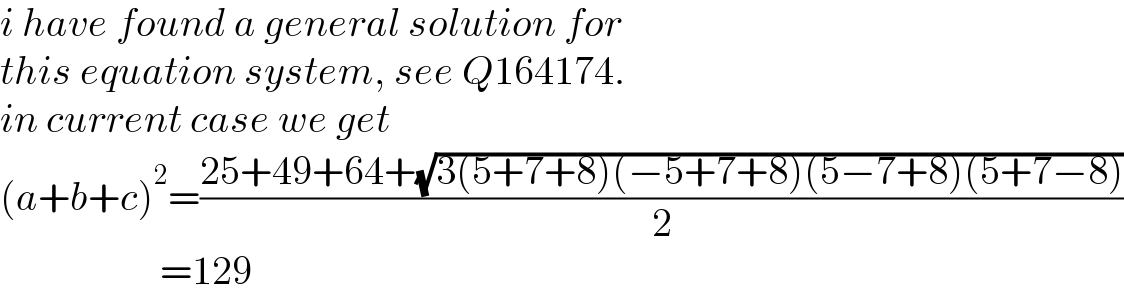
i have found a general solution for this equation system, see Q164174. in current case we get (a+b+c)^2 =((25+49+64+(√(3(5+7+8)(−5+7+8)(5−7+8)(5+7−8))))/2) =129
$${i}\:{have}\:{found}\:{a}\:{general}\:{solution}\:{for} \\ $$$${this}\:{equation}\:{system},\:{see}\:{Q}\mathrm{164174}. \\ $$$${in}\:{current}\:{case}\:{we}\:{get} \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} =\frac{\mathrm{25}+\mathrm{49}+\mathrm{64}+\sqrt{\mathrm{3}\left(\mathrm{5}+\mathrm{7}+\mathrm{8}\right)\left(−\mathrm{5}+\mathrm{7}+\mathrm{8}\right)\left(\mathrm{5}−\mathrm{7}+\mathrm{8}\right)\left(\mathrm{5}+\mathrm{7}−\mathrm{8}\right)}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{129} \\ $$
Answered by SEKRET last updated on 08/Jan/23
{ (((a−b)(a^2 +ab+b^2 )=25(a−b))),(((b−c)(b^2 +bc+c^2 )= 49(b−c))),(( (c−a)(c^2 +ac+a^2 )=64(c−a))) :} + { ((a^3 −b^3 =25a−25b)),((b^3 −c^3 =49b−49c)),((c^3 −a^3 =64c−64a)) :} −39a+24b+15c=0 a = ((5c+8b)/(13)) { (( (((5c+8b)/(13)))^2 +b∙((5c+8b)/(13))+b^2 =25)),((b^2 +bc+c^2 =49)) :} .......... ....
$$\:\:\:\:\begin{cases}{\left(\boldsymbol{\mathrm{a}}−\boldsymbol{\mathrm{b}}\right)\left(\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{ab}}+\boldsymbol{\mathrm{b}}^{\mathrm{2}} \right)=\mathrm{25}\left(\boldsymbol{\mathrm{a}}−\boldsymbol{\mathrm{b}}\right)}\\{\left(\boldsymbol{\mathrm{b}}−\boldsymbol{\mathrm{c}}\right)\left(\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\boldsymbol{\mathrm{bc}}+\boldsymbol{\mathrm{c}}^{\mathrm{2}} \right)=\:\mathrm{49}\left(\boldsymbol{\mathrm{b}}−\boldsymbol{\mathrm{c}}\right)}\\{\:\left(\boldsymbol{\mathrm{c}}−\boldsymbol{\mathrm{a}}\right)\left(\boldsymbol{\mathrm{c}}^{\mathrm{2}} +\boldsymbol{\mathrm{ac}}+\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)=\mathrm{64}\left(\boldsymbol{\mathrm{c}}−\boldsymbol{\mathrm{a}}\right)}\end{cases} \\ $$$$\:\:\:\:\:\:\:\:\:+\:\begin{cases}{\boldsymbol{\mathrm{a}}^{\mathrm{3}} −\boldsymbol{\mathrm{b}}^{\mathrm{3}} =\mathrm{25}\boldsymbol{\mathrm{a}}−\mathrm{25}\boldsymbol{\mathrm{b}}}\\{\boldsymbol{\mathrm{b}}^{\mathrm{3}} −\boldsymbol{\mathrm{c}}^{\mathrm{3}} =\mathrm{49}\boldsymbol{\mathrm{b}}−\mathrm{49}\boldsymbol{\mathrm{c}}}\\{\boldsymbol{\mathrm{c}}^{\mathrm{3}} −\boldsymbol{\mathrm{a}}^{\mathrm{3}} =\mathrm{64}\boldsymbol{\mathrm{c}}−\mathrm{64}\boldsymbol{\mathrm{a}}}\end{cases} \\ $$$$\:\:\:\:\:\:\:\:−\mathrm{39}\boldsymbol{\mathrm{a}}+\mathrm{24}\boldsymbol{\mathrm{b}}+\mathrm{15}\boldsymbol{\mathrm{c}}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\boldsymbol{\mathrm{a}}\:\:=\:\:\frac{\mathrm{5}\boldsymbol{\mathrm{c}}+\mathrm{8}\boldsymbol{\mathrm{b}}}{\mathrm{13}} \\ $$$$\:\:\:\:\:\:\:\begin{cases}{\:\left(\frac{\mathrm{5}\boldsymbol{\mathrm{c}}+\mathrm{8}\boldsymbol{\mathrm{b}}}{\mathrm{13}}\right)^{\mathrm{2}} +\boldsymbol{\mathrm{b}}\centerdot\frac{\mathrm{5}\boldsymbol{\mathrm{c}}+\mathrm{8}\boldsymbol{\mathrm{b}}}{\mathrm{13}}+\boldsymbol{\mathrm{b}}^{\mathrm{2}} =\mathrm{25}}\\{\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\boldsymbol{\mathrm{bc}}+\boldsymbol{\mathrm{c}}^{\mathrm{2}} =\mathrm{49}}\end{cases} \\ $$$$\:\:\:\:\:\:\:\: \\ $$$$………. \\ $$$$…. \\ $$
Answered by SEKRET last updated on 08/Jan/23
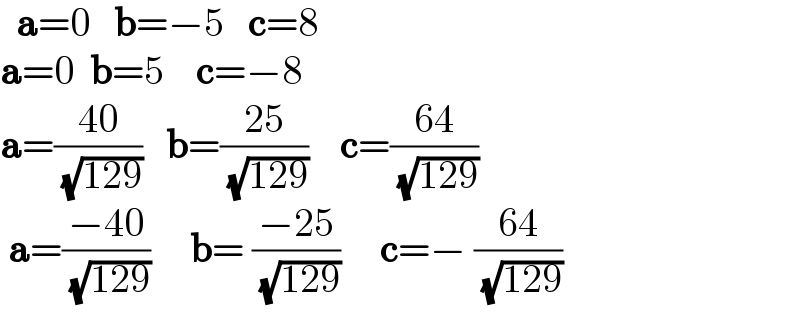
a=0 b=−5 c=8 a=0 b=5 c=−8 a=((40)/( (√(129)))) b=((25)/( (√(129)))) c=((64)/( (√(129)))) a=((−40)/( (√(129)))) b= ((−25)/( (√(129)))) c=− ((64)/( (√(129))))
$$\:\:\boldsymbol{\mathrm{a}}=\mathrm{0}\:\:\:\boldsymbol{\mathrm{b}}=−\mathrm{5}\:\:\:\boldsymbol{\mathrm{c}}=\mathrm{8}\:\:\: \\ $$$$\boldsymbol{\mathrm{a}}=\mathrm{0}\:\:\boldsymbol{\mathrm{b}}=\mathrm{5}\:\:\:\:\boldsymbol{\mathrm{c}}=−\mathrm{8} \\ $$$$\boldsymbol{\mathrm{a}}=\frac{\mathrm{40}}{\:\sqrt{\mathrm{129}}}\:\:\:\boldsymbol{\mathrm{b}}=\frac{\mathrm{25}}{\:\sqrt{\mathrm{129}}}\:\:\:\:\boldsymbol{\mathrm{c}}=\frac{\mathrm{64}}{\:\sqrt{\mathrm{129}}} \\ $$$$\:\boldsymbol{\mathrm{a}}=\frac{−\mathrm{40}}{\:\sqrt{\mathrm{129}}}\:\:\:\:\:\boldsymbol{\mathrm{b}}=\:\frac{−\mathrm{25}}{\:\sqrt{\mathrm{129}}}\:\:\:\:\:\boldsymbol{\mathrm{c}}=−\:\frac{\mathrm{64}}{\:\sqrt{\mathrm{129}}}\: \\ $$
Commented by mr W last updated on 09/Jan/23
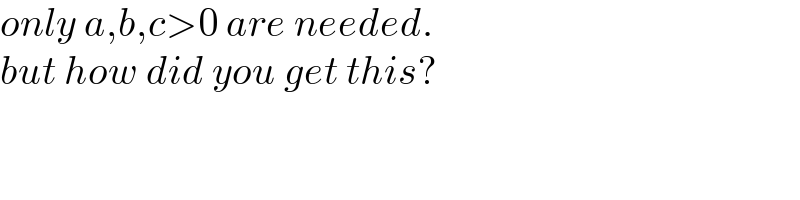
only a,b,c>0 are needed. but how did you get this?
$${only}\:{a},{b},{c}>\mathrm{0}\:{are}\:{needed}. \\ $$$${but}\:{how}\:{did}\:{you}\:{get}\:{this}? \\ $$
Answered by Rasheed.Sindhi last updated on 09/Jan/23
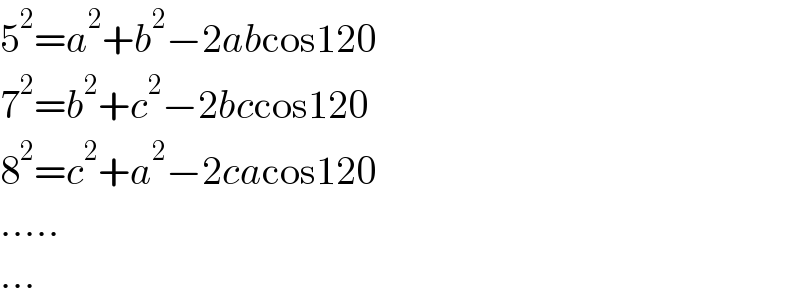
5^2 =a^2 +b^2 −2abcos120 7^2 =b^2 +c^2 −2bccos120 8^2 =c^2 +a^2 −2cacos120 ..... ...
$$\mathrm{5}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\mathrm{cos120} \\ $$$$\mathrm{7}^{\mathrm{2}} ={b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\mathrm{cos120} \\ $$$$\mathrm{8}^{\mathrm{2}} ={c}^{\mathrm{2}} +{a}^{\mathrm{2}} −\mathrm{2}{ca}\mathrm{cos120}\: \\ $$$$….. \\ $$$$… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *