Question Number 184602 by ajfour last updated on 09/Jan/23
Commented by ajfour last updated on 09/Jan/23

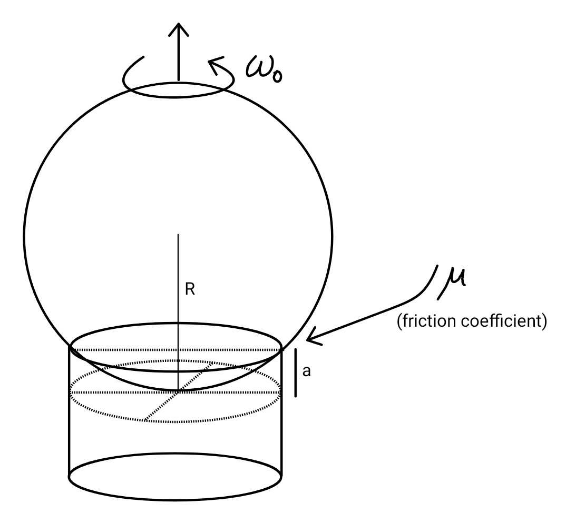
$${If}\:{the}\:{solid}\:{sphere}\:{resting}\:{on} \\ $$$$\:{the}\:{rim}\:{of}\:{a}\:{thin}\:{hollow}\:{fixed}\: \\ $$$${cylinder}\:{is}\:{set}\:{in}\:{motion}\:{at}\:{an}\: \\ $$$${angular}\:{speed}\:\omega_{\mathrm{0}} \:\:{as}\:{shown},\:{then} \\ $$$${find}\:{the}\:{time}\:{it}\:{takes}\:{to}\:{come}\:{to} \\ $$$${a}\:{stop}.\:\:\:{T}={f}\left(\omega_{\mathrm{0}} ,\:{a},\:{R},\:\mu,\:{g}\right) \\ $$
Answered by mr W last updated on 09/Jan/23
Commented by mr W last updated on 09/Jan/23
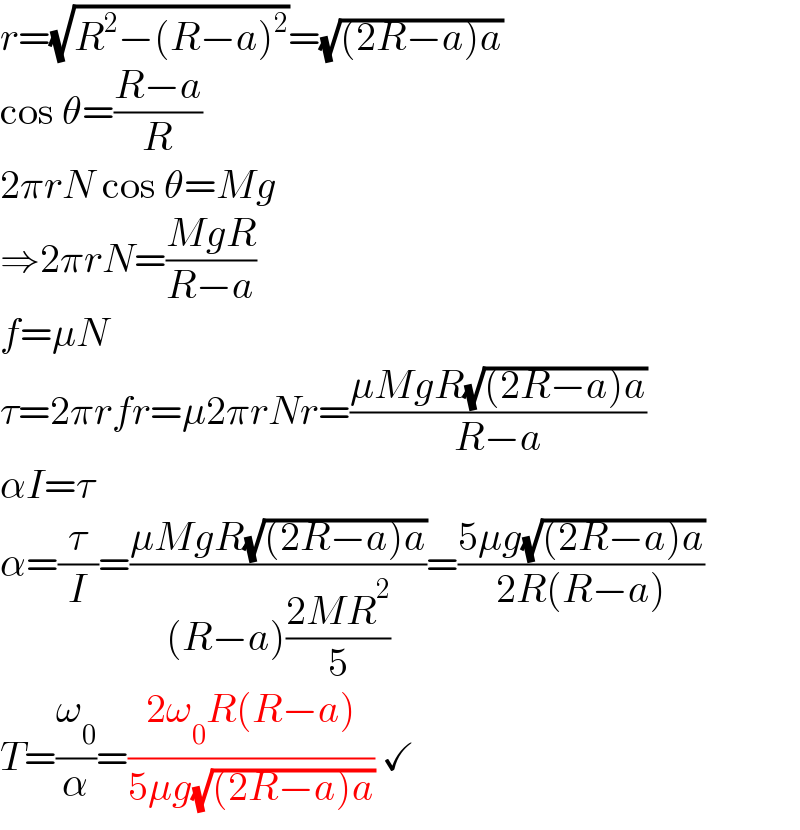
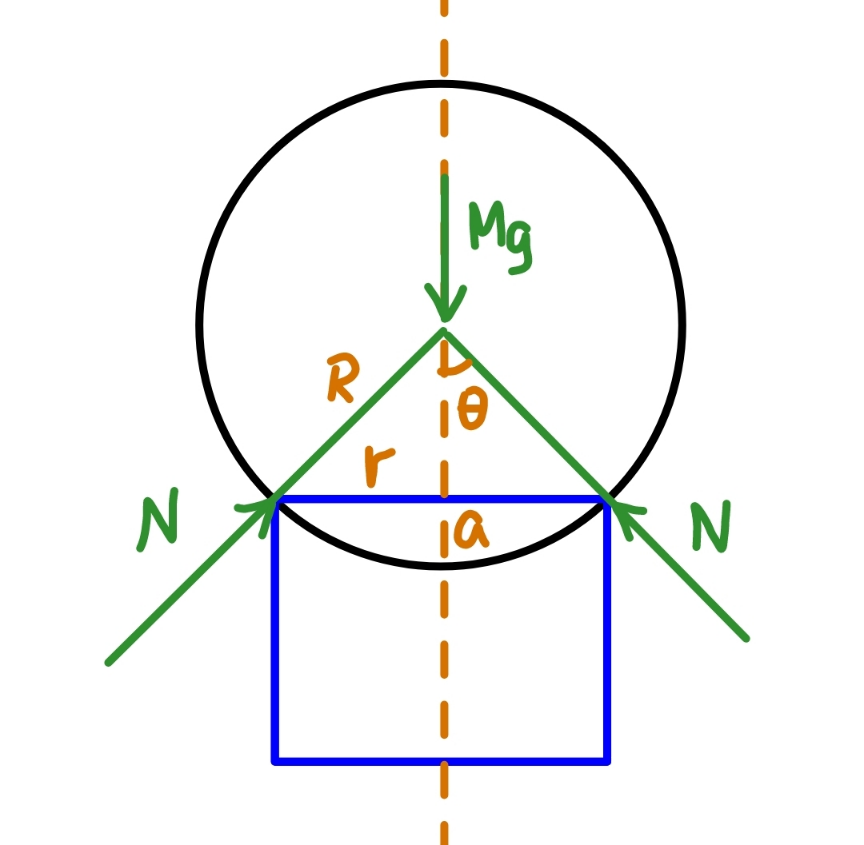
$${r}=\sqrt{{R}^{\mathrm{2}} −\left({R}−{a}\right)^{\mathrm{2}} }=\sqrt{\left(\mathrm{2}{R}−{a}\right){a}} \\ $$$$\mathrm{cos}\:\theta=\frac{{R}−{a}}{{R}} \\ $$$$\mathrm{2}\pi{rN}\:\mathrm{cos}\:\theta={Mg} \\ $$$$\Rightarrow\mathrm{2}\pi{rN}=\frac{{MgR}}{{R}−{a}} \\ $$$${f}=\mu{N} \\ $$$$\tau=\mathrm{2}\pi{rfr}=\mu\mathrm{2}\pi{rNr}=\frac{\mu{MgR}\sqrt{\left(\mathrm{2}{R}−{a}\right){a}}}{{R}−{a}} \\ $$$$\alpha{I}=\tau \\ $$$$\alpha=\frac{\tau}{{I}}=\frac{\mu{MgR}\sqrt{\left(\mathrm{2}{R}−{a}\right){a}}}{\left({R}−{a}\right)\frac{\mathrm{2}{MR}^{\mathrm{2}} }{\mathrm{5}}}=\frac{\mathrm{5}\mu{g}\sqrt{\left(\mathrm{2}{R}−{a}\right){a}}}{\mathrm{2}{R}\left({R}−{a}\right)} \\ $$$${T}=\frac{\omega_{\mathrm{0}} }{\alpha}=\frac{\mathrm{2}\omega_{\mathrm{0}} {R}\left({R}−{a}\right)}{\mathrm{5}\mu{g}\sqrt{\left(\mathrm{2}{R}−{a}\right){a}}}\:\checkmark \\ $$
Commented by ajfour last updated on 09/Jan/23
$${Indeed},\:{beautiful}\:{solution}\:{Sir}! \\ $$
