Question Number 18461 by b.e.h.i.8.3.417@gmail.com last updated on 22/Jul/17

Answered by mrW1 last updated on 22/Jul/17
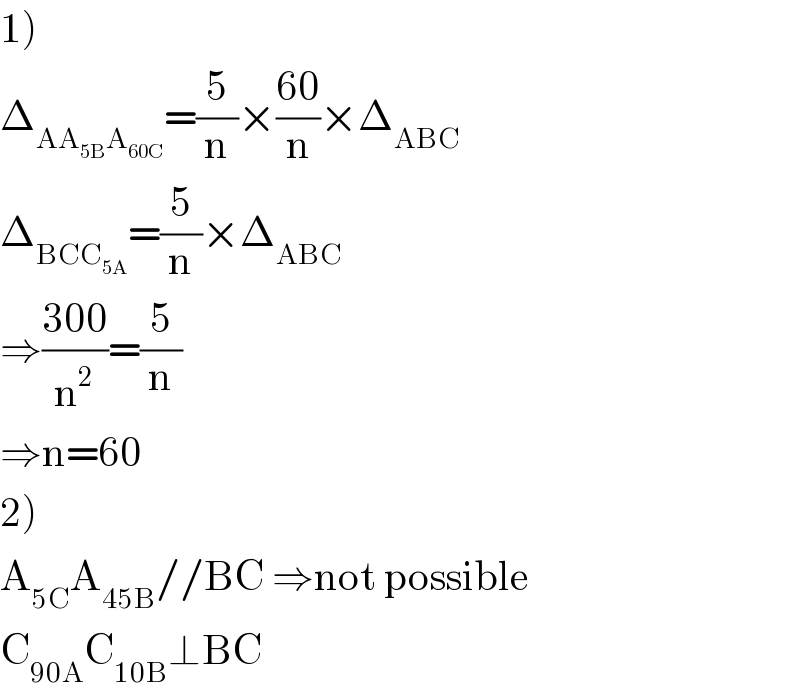
$$\left.\mathrm{1}\right) \\ $$$$\Delta_{\mathrm{AA}_{\mathrm{5B}} \mathrm{A}_{\mathrm{60C}} } =\frac{\mathrm{5}}{\mathrm{n}}×\frac{\mathrm{60}}{\mathrm{n}}×\Delta_{\mathrm{ABC}} \\ $$$$\Delta_{\mathrm{BCC}_{\mathrm{5A}} } =\frac{\mathrm{5}}{\mathrm{n}}×\Delta_{\mathrm{ABC}} \\ $$$$\Rightarrow\frac{\mathrm{300}}{\mathrm{n}^{\mathrm{2}} }=\frac{\mathrm{5}}{\mathrm{n}} \\ $$$$\Rightarrow\mathrm{n}=\mathrm{60} \\ $$$$\left.\mathrm{2}\right) \\ $$$$\mathrm{A}_{\mathrm{5C}} \mathrm{A}_{\mathrm{45B}} //\mathrm{BC}\:\Rightarrow\mathrm{not}\:\mathrm{possible} \\ $$$$\mathrm{C}_{\mathrm{90A}} \mathrm{C}_{\mathrm{10B}} \bot\mathrm{BC} \\ $$
Commented by b.e.h.i.8.3.417@gmail.com last updated on 22/Jul/17
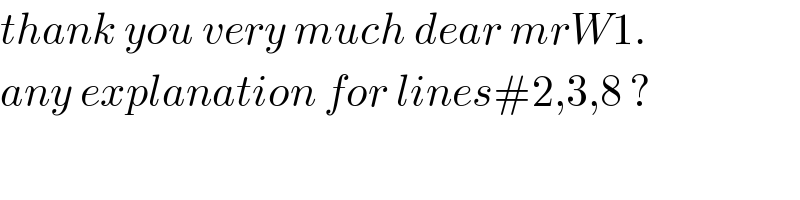
$${thank}\:{you}\:{very}\:{much}\:{dear}\:{mrW}\mathrm{1}. \\ $$$${any}\:{explanation}\:{for}\:{lines}#\mathrm{2},\mathrm{3},\mathrm{8}\:? \\ $$$$ \\ $$
Commented by mrW1 last updated on 22/Jul/17

Commented by mrW1 last updated on 23/Jul/17
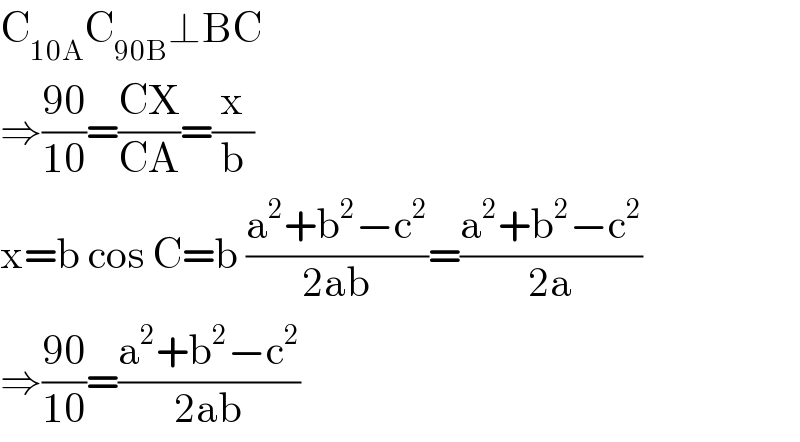
$$\mathrm{C}_{\mathrm{10A}} \mathrm{C}_{\mathrm{90B}} \bot\mathrm{BC} \\ $$$$\Rightarrow\frac{\mathrm{90}}{\mathrm{10}}=\frac{\mathrm{CX}}{\mathrm{CA}}=\frac{\mathrm{x}}{\mathrm{b}} \\ $$$$\mathrm{x}=\mathrm{b}\:\mathrm{cos}\:\mathrm{C}=\mathrm{b}\:\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} }{\mathrm{2ab}}=\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} }{\mathrm{2a}} \\ $$$$\Rightarrow\frac{\mathrm{90}}{\mathrm{10}}=\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} }{\mathrm{2ab}} \\ $$
Commented by mrW1 last updated on 23/Jul/17

