Question Number 184822 by mnjuly1970 last updated on 12/Jan/23
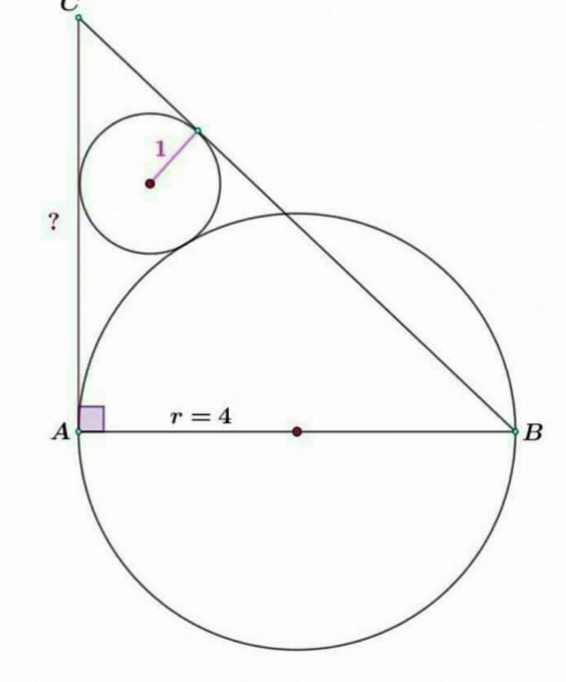
Answered by mr W last updated on 12/Jan/23
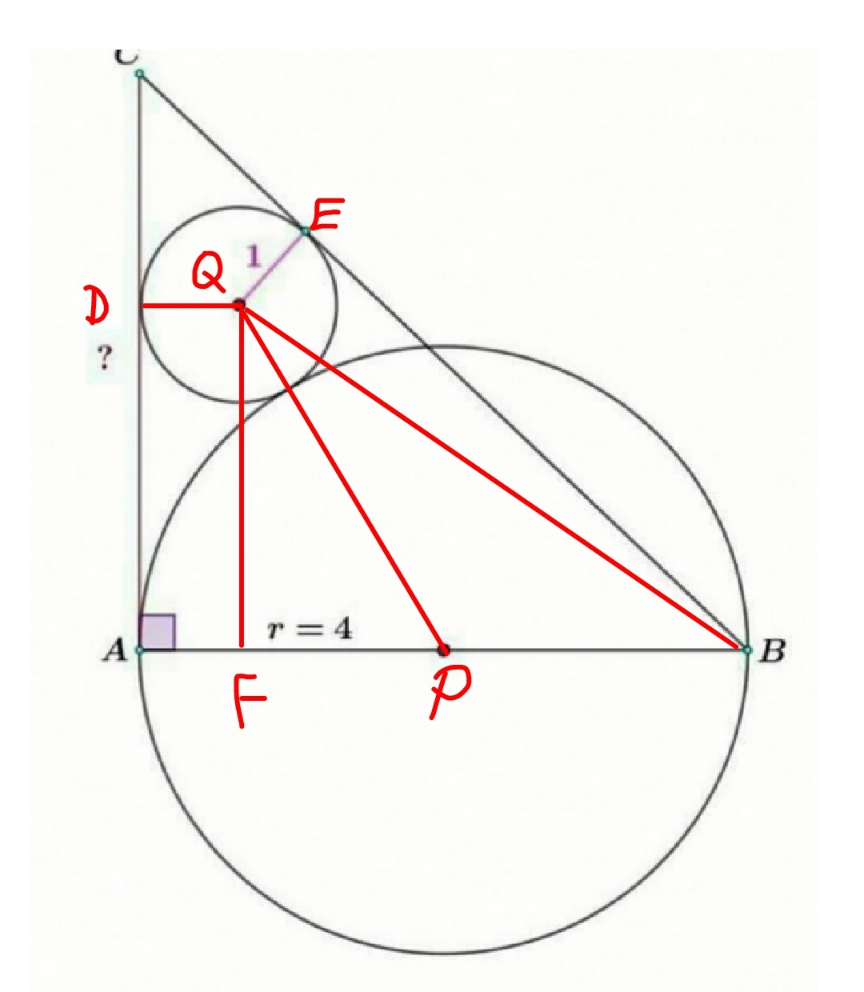
Commented by mr W last updated on 12/Jan/23
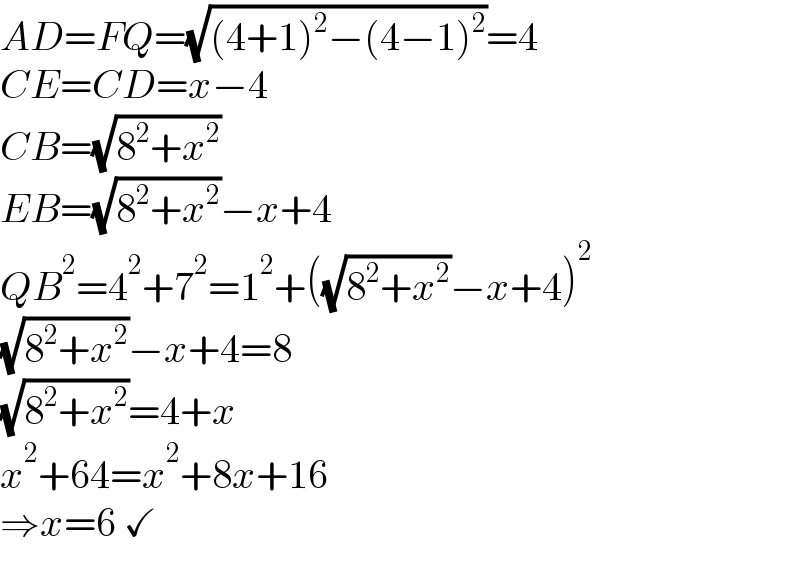
$${AD}={FQ}=\sqrt{\left(\mathrm{4}+\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{4}−\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{4} \\ $$$${CE}={CD}={x}−\mathrm{4} \\ $$$${CB}=\sqrt{\mathrm{8}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$${EB}=\sqrt{\mathrm{8}^{\mathrm{2}} +{x}^{\mathrm{2}} }−{x}+\mathrm{4} \\ $$$${QB}^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} +\left(\sqrt{\mathrm{8}^{\mathrm{2}} +{x}^{\mathrm{2}} }−{x}+\mathrm{4}\right)^{\mathrm{2}} \\ $$$$\sqrt{\mathrm{8}^{\mathrm{2}} +{x}^{\mathrm{2}} }−{x}+\mathrm{4}=\mathrm{8} \\ $$$$\sqrt{\mathrm{8}^{\mathrm{2}} +{x}^{\mathrm{2}} }=\mathrm{4}+{x} \\ $$$${x}^{\mathrm{2}} +\mathrm{64}={x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{16} \\ $$$$\Rightarrow{x}=\mathrm{6}\:\checkmark \\ $$
Commented by mnjuly1970 last updated on 12/Jan/23
$$\:{peace}\:{be}\:{upon}\:{you}\:{Sir}\:\:{W} \\ $$
