Question Number 184841 by Shrinava last updated on 12/Jan/23

Answered by manolex last updated on 12/Jan/23
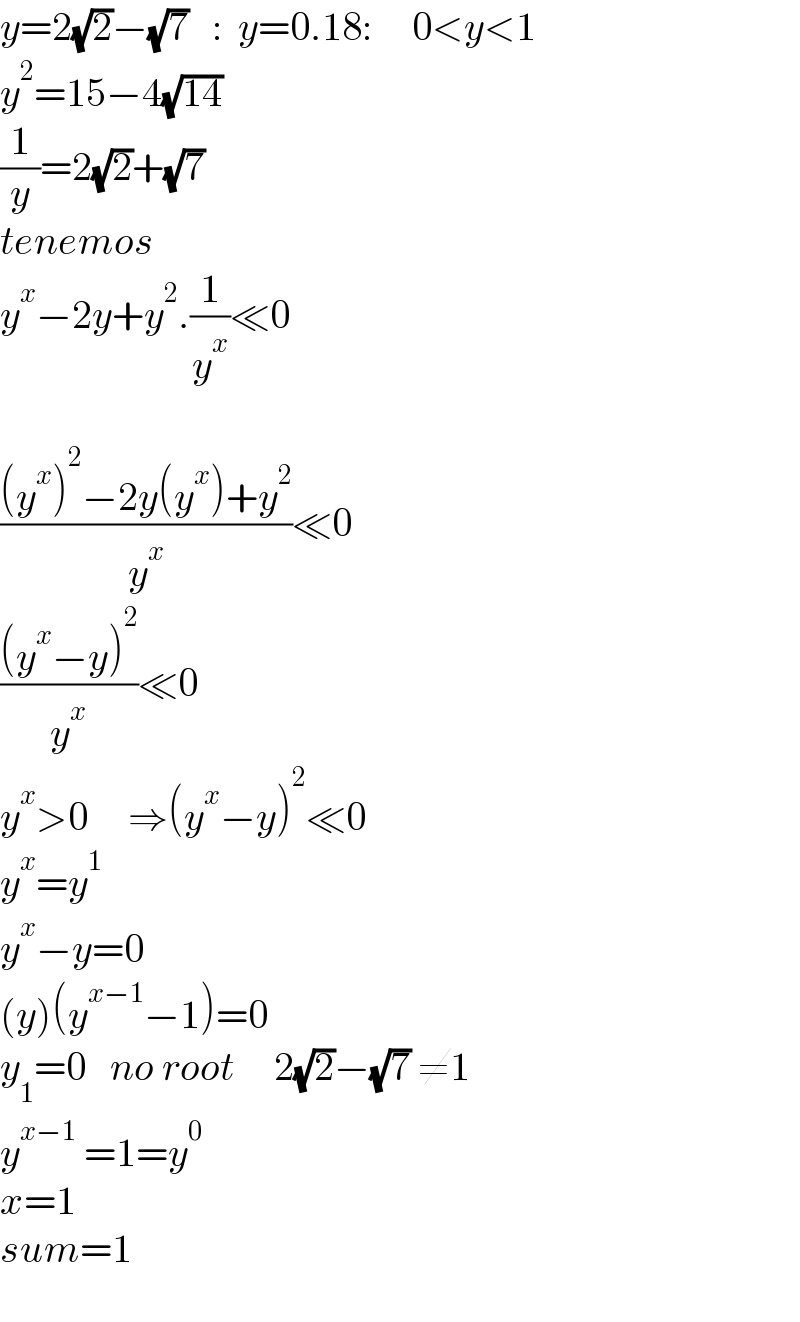
$${y}=\mathrm{2}\sqrt{\mathrm{2}}−\sqrt{\mathrm{7}}\:\:\::\:\:{y}=\mathrm{0}.\mathrm{18}:\:\:\:\:\:\mathrm{0}<{y}<\mathrm{1} \\ $$$${y}^{\mathrm{2}} =\mathrm{15}−\mathrm{4}\sqrt{\mathrm{14}} \\ $$$$\frac{\mathrm{1}}{{y}}=\mathrm{2}\sqrt{\mathrm{2}}+\sqrt{\mathrm{7}} \\ $$$${tenemos} \\ $$$${y}^{{x}} −\mathrm{2}{y}+{y}^{\mathrm{2}} .\frac{\mathrm{1}}{{y}^{{x}} }\ll\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\frac{\left({y}^{{x}} \right)^{\mathrm{2}} −\mathrm{2}{y}\left({y}^{{x}} \right)+{y}^{\mathrm{2}} }{{y}^{{x}} }\ll\mathrm{0} \\ $$$$\frac{\left({y}^{{x}} −{y}\right)^{\mathrm{2}} }{{y}^{{x}} }\ll\mathrm{0} \\ $$$${y}^{{x}} >\mathrm{0}\:\:\:\:\:\Rightarrow\left({y}^{{x}} −{y}\right)^{\mathrm{2}} \ll\mathrm{0} \\ $$$${y}^{{x}} ={y}^{\mathrm{1}} \\ $$$${y}^{{x}} −{y}=\mathrm{0} \\ $$$$\left({y}\right)\left({y}^{{x}−\mathrm{1}} −\mathrm{1}\right)=\mathrm{0} \\ $$$${y}_{\mathrm{1}} =\mathrm{0}\:\:\:{no}\:{root}\:\:\:\:\:\mathrm{2}\sqrt{\mathrm{2}}−\sqrt{\mathrm{7}}\:\neq\mathrm{1} \\ $$$${y}^{{x}−\mathrm{1}} \:=\mathrm{1}={y}^{\mathrm{0}} \\ $$$${x}=\mathrm{1} \\ $$$${sum}=\mathrm{1} \\ $$$$ \\ $$
