Question Number 184866 by paul2222 last updated on 12/Jan/23
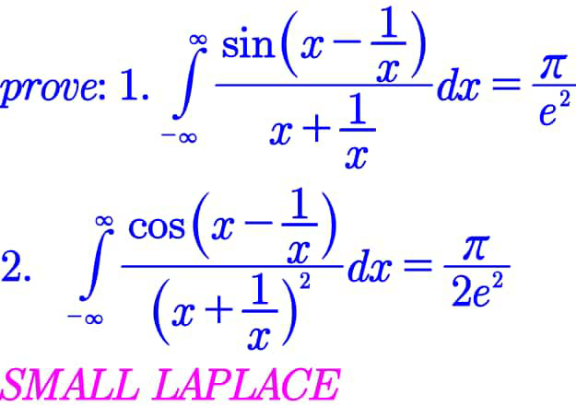
Commented by Frix last updated on 13/Jan/23

$$\mathrm{Waiting}… \\ $$$$\boldsymbol{{BIG}}\:\boldsymbol{{GODOT}} \\ $$
Answered by Mathspace last updated on 13/Jan/23

$${I}=\int_{−\infty} ^{+\infty} \frac{{sin}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{{x}+\frac{\mathrm{1}}{{x}}}\:{dx} \\ $$$${I}=\int_{−\infty} ^{−\infty} \:\frac{{sin}\left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}}\right)}{\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}}}{dx} \\ $$$$=\int_{−\infty} ^{\infty} \frac{{xsin}\left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$=\:{Im}\left(\int_{−\infty} ^{+\infty} \frac{{xe}^{{i}\left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}}\right)} }{{x}^{\mathrm{2}} +\mathrm{1}}{dx}\right) \\ $$$${let}\:{f}\left({z}\right)=\frac{{ze}^{{i}\left(\frac{{z}^{\mathrm{2}} −\mathrm{1}}{{z}}\right)} }{{z}^{\mathrm{2}} +\mathrm{1}}=\frac{{ze}^{{i}\left(\frac{{z}^{\mathrm{2}} −\mathrm{1}}{{z}}\right)} }{\left({z}−{i}\right)\left({z}+{i}\right)} \\ $$$${the}\:\rho{oles}\:{of}\:\:\varphi\:{are}\:{i}\:{and}\:−{i} \\ $$$${residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \:{f}\left({z}\right){dz}=\mathrm{2}{i}\pi{Res}\left({f},{i}\right) \\ $$$$=\mathrm{2}{i}\pi.\frac{{ie}^{{i}\left(\frac{{i}^{\mathrm{2}} −\mathrm{1}}{{i}}\right)} }{\mathrm{2}{i}}={i}\pi\:{e}^{−\mathrm{2}} =\frac{{i}\pi}{{e}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\:{I}=\frac{\pi}{{e}^{\mathrm{2}} } \\ $$
