Menu Close

Question-184875

Tinku Tara 0 Comments
Pin




Question Number 184875 by universe last updated on 13/Jan/23
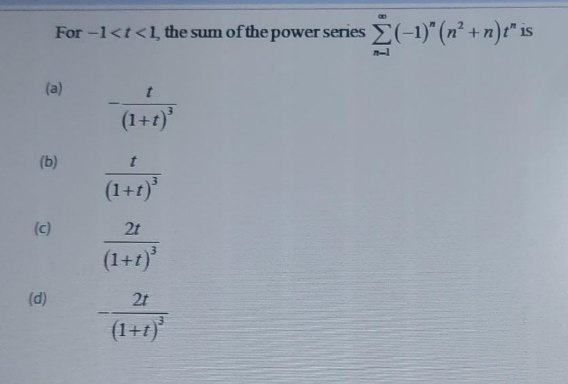
Answered by Mathspace last updated on 13/Jan/23
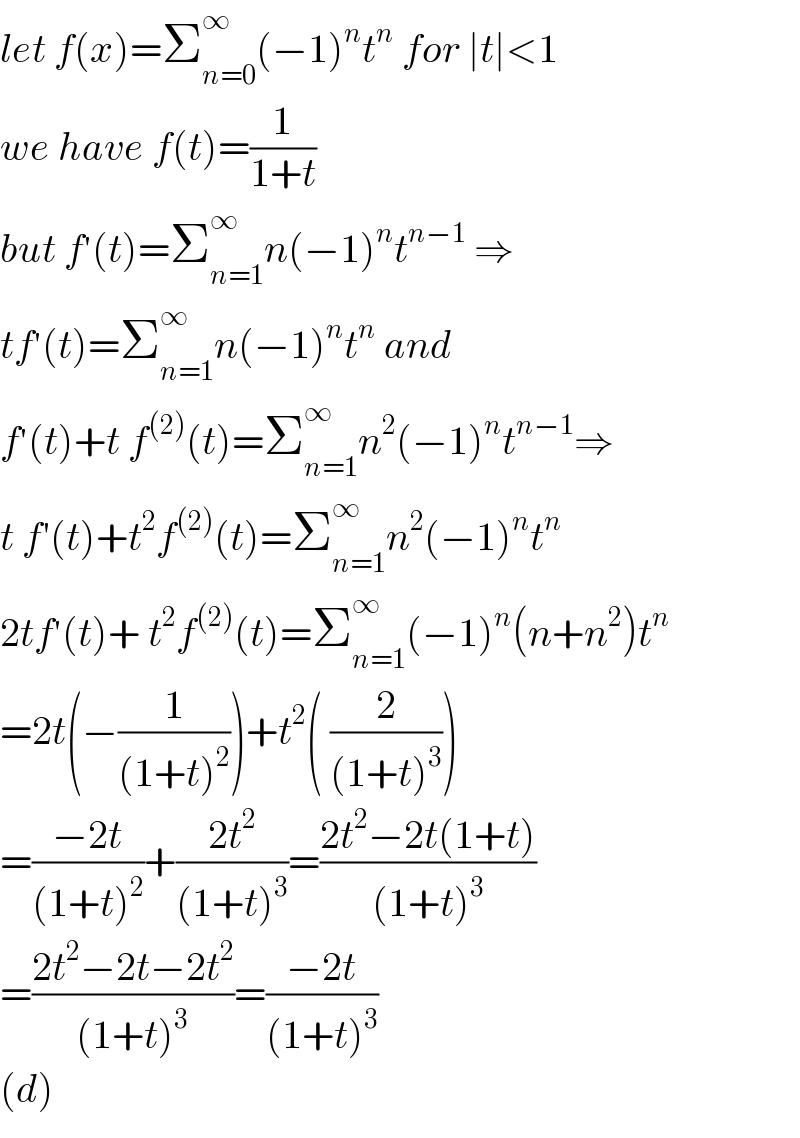
let f(x)=Σ_(n=0) ^∞ (−1)^n t^n for ∣t∣<1 we have f(t)=(1/(1+t)) but f^′ (t)=Σ_(n=1) ^∞ n(−1)^n t^(n−1) ⇒ tf^′ (t)=Σ_(n=1) ^∞ n(−1)^n t^n and f^′ (t)+t f^((2)) (t)=Σ_(n=1) ^∞ n^2 (−1)^n t^(n−1) ⇒ t f′(t)+t^2 f^((2)) (t)=Σ_(n=1) ^∞ n^2 (−1)^n t^n 2tf^′ (t)+ t^2 f^((2)) (t)=Σ_(n=1) ^∞ (−1)^n (n+n^2 )t^n =2t(−(1/((1+t)^2 )))+t^2 ( (2/((1+t)^3 ))) =((−2t)/((1+t)^2 ))+((2t^2 )/((1+t)^3 ))=((2t^2 −2t(1+t))/((1+t)^3 )) =((2t^2 −2t−2t^2 )/((1+t)^3 ))=((−2t)/((1+t)^3 )) (d)
$${let}\:{f}\left({x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {t}^{{n}} \:{for}\:\mid{t}\mid<\mathrm{1} \\ $$$${we}\:{have}\:{f}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{1}+{t}} \\ $$$${but}\:{f}^{'} \left({t}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} {n}\left(−\mathrm{1}\right)^{{n}} {t}^{{n}−\mathrm{1}} \:\Rightarrow \\ $$$${tf}^{'} \left({t}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} {n}\left(−\mathrm{1}\right)^{{n}} {t}^{{n}} \:{and} \\ $$$${f}^{'} \left({t}\right)+{t}\:{f}^{\left(\mathrm{2}\right)} \left({t}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} {n}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{n}} {t}^{{n}−\mathrm{1}} \Rightarrow \\ $$$${t}\:{f}'\left({t}\right)+{t}^{\mathrm{2}} {f}^{\left(\mathrm{2}\right)} \left({t}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} {n}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{n}} {t}^{{n}} \\ $$$$\mathrm{2}{tf}^{'} \left({t}\right)+\:{t}^{\mathrm{2}} {f}^{\left(\mathrm{2}\right)} \left({t}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \left({n}+{n}^{\mathrm{2}} \right){t}^{{n}} \\ $$$$=\mathrm{2}{t}\left(−\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\right)+{t}^{\mathrm{2}} \left(\:\frac{\mathrm{2}}{\left(\mathrm{1}+{t}\right)^{\mathrm{3}} }\right) \\ $$$$=\frac{−\mathrm{2}{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}\right)^{\mathrm{3}} }=\frac{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{t}\left(\mathrm{1}+{t}\right)}{\left(\mathrm{1}+{t}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{2}{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}\right)^{\mathrm{3}} }=\frac{−\mathrm{2}{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{3}} } \\ $$$$\left({d}\right) \\ $$
Commented by universe last updated on 13/Jan/23
thank you sir
$${thank}\:{you}\:{sir} \\ $$$$ \\ $$
Commented by Mathspace last updated on 13/Jan/23
you are welcome
$${you}\:{are}\:{welcome} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *