Question Number 184955 by mnjuly1970 last updated on 14/Jan/23
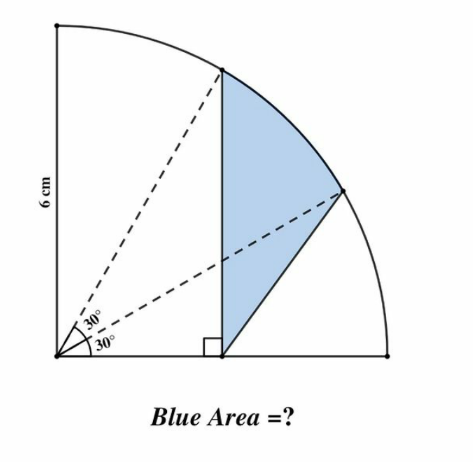
Answered by HeferH last updated on 14/Jan/23
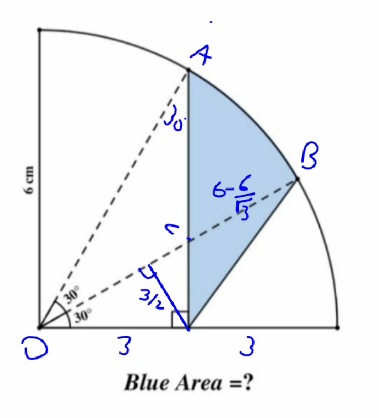
Commented by HeferH last updated on 14/Jan/23
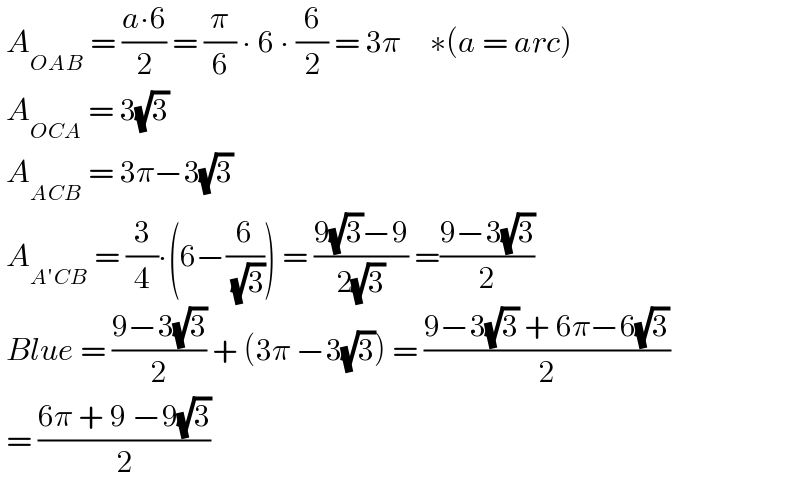
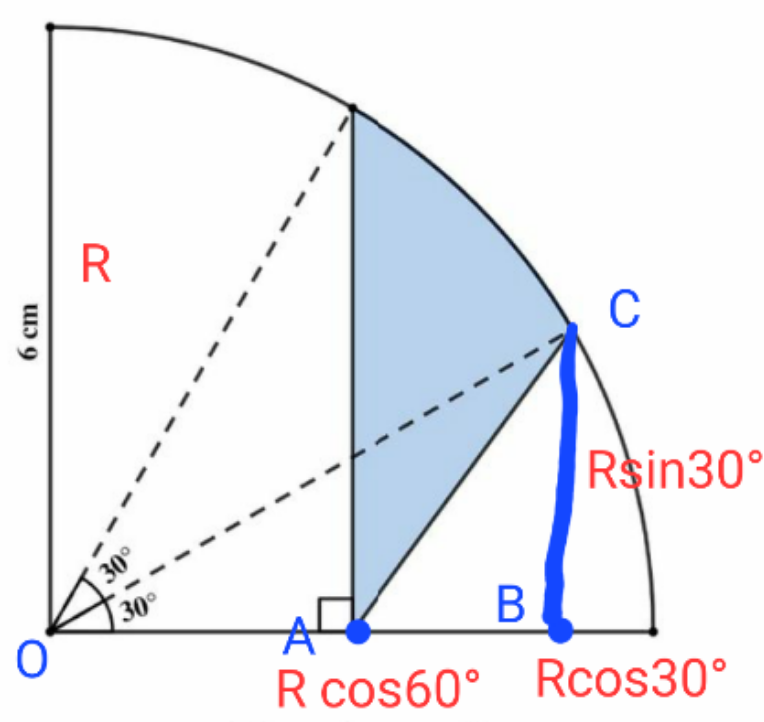
$$\:{A}_{{OAB}} \:=\:\frac{{a}\centerdot\mathrm{6}}{\mathrm{2}}\:=\:\frac{\pi}{\mathrm{6}}\:\centerdot\:\mathrm{6}\:\centerdot\:\frac{\mathrm{6}}{\mathrm{2}}\:=\:\mathrm{3}\pi\:\:\:\:\:\ast\left({a}\:=\:{arc}\right)\: \\ $$$$\:{A}_{{OCA}} \:=\:\mathrm{3}\sqrt{\mathrm{3}} \\ $$$$\:{A}_{{ACB}} \:=\:\mathrm{3}\pi−\mathrm{3}\sqrt{\mathrm{3}} \\ $$$$\:{A}_{{A}'{CB}} \:=\:\frac{\mathrm{3}}{\mathrm{4}}\centerdot\left(\mathrm{6}−\frac{\mathrm{6}}{\:\sqrt{\mathrm{3}}}\right)\:=\:\frac{\mathrm{9}\sqrt{\mathrm{3}}−\mathrm{9}}{\mathrm{2}\sqrt{\mathrm{3}}}\:=\frac{\mathrm{9}−\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\:{Blue}\:=\:\frac{\mathrm{9}−\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\:+\:\left(\mathrm{3}\pi\:−\mathrm{3}\sqrt{\mathrm{3}}\right)\:=\:\frac{\mathrm{9}−\mathrm{3}\sqrt{\mathrm{3}}\:+\:\mathrm{6}\pi−\mathrm{6}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\:=\:\frac{\mathrm{6}\pi\:+\:\mathrm{9}\:−\mathrm{9}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
Answered by JDamian last updated on 15/Jan/23
![a=∣OA^(→) ∣=R cos 60°=(R/2) b=∣OB^(→) ∣=R cos 30°=((√3)/2)R ∣AB^(→) ∣=b−a=(((√3)−1)/2)R S_(blue) =∫_a ^b (√(R^2 −x^2 ))dx−S_(ABC^(△) ) S_(ABC^(△) ) =(1/2)∣AB^(→) ∣∙R∙sin 30°=(R^2 /8)((√3)−1) ∫_a ^b (√(R^2 −x^2 ))dx= = determinant (((x=R∙sinϕ),→,(dx=R∙cosϕdϕ)),((a=(R/2)=R∙sin((π/6))),→,(ϕ_a =(π/6))),((b=R((√3)/2)=R∙sin((π/3))),→,(ϕ_b =(π/3))))= =∫_(π/6) ^(π/3) R^2 cos^2 ϕdϕ=(R^2 /2)[ϕ+((sin2ϕ)/2)]_(π/6) ^(π/3) = =(R^2 /2)((π/3)−(π/6))=(π/(12))R^2 S_(blue) =R^2 ((π/(12))−(((√3)−1)/8))=((R/2))^2 ((π/3)−(((√3)−1)/2)) ■](https://www.tinkutara.com/question/Q184985.png)
$$ \\ $$$${a}=\mid\overset{\rightarrow} {{OA}}\mid={R}\:\mathrm{cos}\:\mathrm{60}°=\frac{{R}}{\mathrm{2}} \\ $$$${b}=\mid\overset{\rightarrow} {{OB}}\mid={R}\:\mathrm{cos}\:\:\mathrm{30}°=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{R} \\ $$$$\mid\overset{\rightarrow} {{AB}}\mid={b}−{a}=\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}{R} \\ $$$${S}_{{blue}} =\int_{{a}} ^{{b}} \sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}−{S}_{\overset{\bigtriangleup} {{ABC}}} \\ $$$${S}_{\overset{\bigtriangleup} {{ABC}}} =\frac{\mathrm{1}}{\mathrm{2}}\mid\overset{\rightarrow} {{AB}}\mid\centerdot{R}\centerdot\mathrm{sin}\:\mathrm{30}°=\frac{{R}^{\mathrm{2}} }{\mathrm{8}}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right) \\ $$$$ \\ $$$$\int_{{a}} ^{{b}} \sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}= \\ $$$$=\begin{vmatrix}{{x}={R}\centerdot\mathrm{sin}\varphi}&{\rightarrow}&{{dx}={R}\centerdot\mathrm{cos}\varphi{d}\varphi}\\{{a}=\frac{{R}}{\mathrm{2}}={R}\centerdot\mathrm{sin}\left(\frac{\pi}{\mathrm{6}}\right)}&{\rightarrow}&{\varphi_{{a}} =\frac{\pi}{\mathrm{6}}}\\{{b}={R}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}={R}\centerdot\mathrm{sin}\left(\frac{\pi}{\mathrm{3}}\right)}&{\rightarrow}&{\varphi_{{b}} =\frac{\pi}{\mathrm{3}}}\end{vmatrix}= \\ $$$$=\int_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} {R}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \varphi{d}\varphi=\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left[\varphi+\frac{\mathrm{sin2}\varphi}{\mathrm{2}}\right]_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} = \\ $$$$=\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\pi}{\mathrm{3}}−\frac{\pi}{\mathrm{6}}\right)=\frac{\pi}{\mathrm{12}}{R}^{\mathrm{2}} \\ $$$$ \\ $$$${S}_{{blue}} ={R}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{12}}−\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{8}}\right)=\left(\frac{{R}}{\mathrm{2}}\right)^{\mathrm{2}} \left(\frac{\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}\right)\:\blacksquare \\ $$
Commented by JDamian last updated on 15/Jan/23