Question Number 184959 by Noorzai last updated on 14/Jan/23

Answered by manxsol last updated on 14/Jan/23
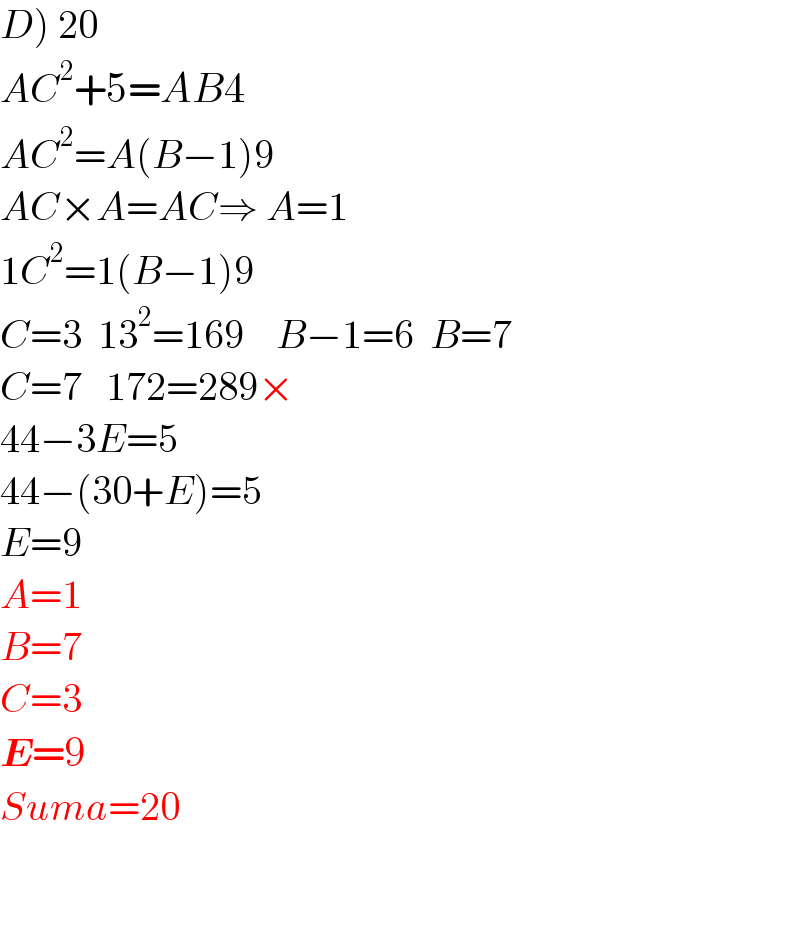
$$\left.{D}\right)\:\mathrm{20} \\ $$$${AC}^{\mathrm{2}} +\mathrm{5}={AB}\mathrm{4} \\ $$$${AC}^{\mathrm{2}} ={A}\left({B}−\mathrm{1}\right)\mathrm{9} \\ $$$${AC}×{A}={AC}\Rightarrow\:{A}=\mathrm{1} \\ $$$$\mathrm{1}{C}^{\mathrm{2}} =\mathrm{1}\left({B}−\mathrm{1}\right)\mathrm{9} \\ $$$${C}=\mathrm{3}\:\:\mathrm{13}^{\mathrm{2}} =\mathrm{169}\:\:\:\:{B}−\mathrm{1}=\mathrm{6}\:\:{B}=\mathrm{7} \\ $$$${C}=\mathrm{7}\:\:\:\mathrm{172}=\mathrm{289}× \\ $$$$\mathrm{44}−\mathrm{3}{E}=\mathrm{5} \\ $$$$\mathrm{44}−\left(\mathrm{30}+{E}\right)=\mathrm{5} \\ $$$${E}=\mathrm{9} \\ $$$${A}=\mathrm{1} \\ $$$${B}=\mathrm{7} \\ $$$${C}=\mathrm{3} \\ $$$$\boldsymbol{{E}}=\mathrm{9} \\ $$$${Suma}=\mathrm{20} \\ $$$$ \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 14/Jan/23

$$\mathrm{AB4}\:\:\mathrm{is}\:\:\mathrm{dividend},\mathrm{AC}\:\mathrm{is}\:\mathrm{divisor}\:\mathrm{and}\: \\ $$$$\mathrm{5}\:\mathrm{is}\:\mathrm{remainder}. \\ $$$$\underline{\mathrm{44}−\mathrm{CE}=\mathrm{05}:} \\ $$$$\mathrm{5}\:\mathrm{comes}\:\mathrm{out}\:\mathrm{of}\:\:\left(\mathrm{4}+\mathrm{borrow}=\mathrm{14}\right)−\mathrm{E} \\ $$$$\mathrm{14}−\mathrm{E}=\mathrm{5}\Rightarrow\mathrm{E}=\mathrm{9} \\ $$$$\mathrm{3}−\mathrm{C}=\mathrm{0}\Rightarrow\mathrm{C}=\mathrm{3} \\ $$$$\:\:\:\:\underset{\underline{−\mathrm{AC}\:\:}\:\:\:} {\mathrm{AB}4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}\:\:\:\mathrm{4} \\ $$$$\mathrm{B}−\mathrm{C}=\mathrm{4}\Rightarrow\mathrm{B}−\mathrm{3}=\mathrm{4}\Rightarrow\mathrm{B}=\mathrm{7} \\ $$$$\mathrm{AC}\:\mid\:\mathrm{CE}\Rightarrow\:\mathrm{A3}\:\mid\mathrm{39}\Rightarrow\mathrm{A}=\mathrm{1} \\ $$$$\mathrm{A}+\mathrm{B}+\mathrm{C}+\mathrm{E}=\mathrm{1}+\mathrm{7}+\mathrm{3}+\mathrm{9}=\mathrm{20} \\ $$
