Question Number 184988 by saboorhalimi last updated on 15/Jan/23
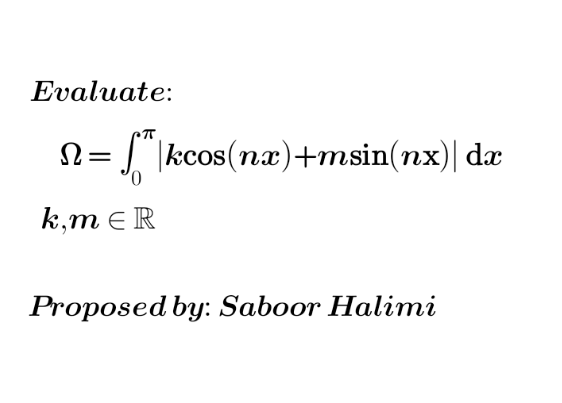
Answered by a.lgnaoui last updated on 15/Jan/23
![Ω=∫_0 ^(π/2) (kcos (nx)+msin nx)dx+ ∫_(π/2) ^π (kcos (nx)+msin nx)dx =[(k/n)sin nx−(m/n)cos nx]_0 ^(π/2) + [(k/n)sin nx−(m/n)cos nx]_(π/2) ^π = (1/n)[(ksin ((nπ)/2)−mcos ((πn)/2))]_0 ^(π/2) + (1/n)[(ksin ((πn)/2)−mcos ((πn)/2))]_(π/2) ^π p>0 n pair Ω=0 Ω= (m/n)(√2) p≥1 ( n impair) Ω= (k/n)+(k/n)[sin (nx)]_(π/2) ^π =(k/n)−(k/n)=0](https://www.tinkutara.com/question/Q185003.png)
$$\Omega=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({k}\mathrm{cos}\:\left({nx}\right)+{m}\mathrm{sin}\:{nx}\right){dx}+ \\ $$$$\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \left({k}\mathrm{cos}\:\left({nx}\right)+{m}\mathrm{sin}\:{nx}\right){dx} \\ $$$$=\left[\frac{{k}}{{n}}\mathrm{sin}\:{nx}−\frac{{m}}{{n}}\mathrm{cos}\:{nx}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} + \\ $$$$\:\:\left[\frac{{k}}{{n}}\mathrm{sin}\:{nx}−\frac{{m}}{{n}}\mathrm{cos}\:{nx}\right]_{\frac{\pi}{\mathrm{2}}} ^{\pi} = \\ $$$$\frac{\mathrm{1}}{\boldsymbol{{n}}}\left[\left({k}\mathrm{sin}\:\frac{{n}\pi}{\mathrm{2}}−{m}\mathrm{cos}\:\frac{\pi{n}}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} + \\ $$$$\frac{\mathrm{1}}{{n}}\left[\left({k}\mathrm{sin}\:\frac{\pi{n}}{\mathrm{2}}−{m}\mathrm{cos}\:\frac{\pi{n}}{\mathrm{2}}\right)\right]_{\frac{\pi}{\mathrm{2}}} ^{\pi} \\ $$$$ \\ $$$${p}>\mathrm{0}\:\:\:{n}\:{pair}\:\:\Omega=\mathrm{0} \\ $$$$\:\:\Omega=\:\:\frac{{m}}{{n}}\sqrt{\mathrm{2}} \\ $$$${p}\geqslant\mathrm{1}\:\left(\:{n}\:{impair}\right) \\ $$$$\:\Omega=\:\frac{{k}}{{n}}+\frac{{k}}{{n}}\left[\mathrm{sin}\:\left({nx}\right)\right]_{\frac{\pi}{\mathrm{2}}} ^{\pi} =\frac{{k}}{{n}}−\frac{{k}}{{n}}=\mathrm{0} \\ $$$$ \\ $$
Commented by Frix last updated on 15/Jan/23
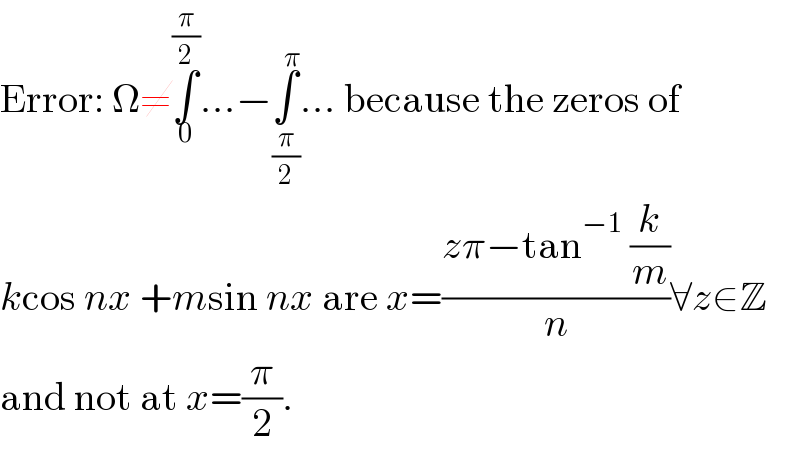
$$\mathrm{Error}:\:\Omega\neq\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}…−\underset{\frac{\pi}{\mathrm{2}}} {\overset{\pi} {\int}}…\:\mathrm{because}\:\mathrm{the}\:\mathrm{zeros}\:\mathrm{of} \\ $$$${k}\mathrm{cos}\:{nx}\:+{m}\mathrm{sin}\:{nx}\:\mathrm{are}\:{x}=\frac{{z}\pi−\mathrm{tan}^{−\mathrm{1}} \:\frac{{k}}{{m}}}{{n}}\forall{z}\in\mathbb{Z} \\ $$$$\mathrm{and}\:\mathrm{not}\:\mathrm{at}\:{x}=\frac{\pi}{\mathrm{2}}. \\ $$
Commented by saboorhalimi last updated on 16/Jan/23

$$\:\:\:\:\:\:\boldsymbol{\mathrm{please}}\:\:\boldsymbol{\mathrm{check}}\:\:\boldsymbol{\mathrm{your}}\:\:\boldsymbol{\mathrm{solution}}\:\boldsymbol{\mathrm{again}} \\ $$
