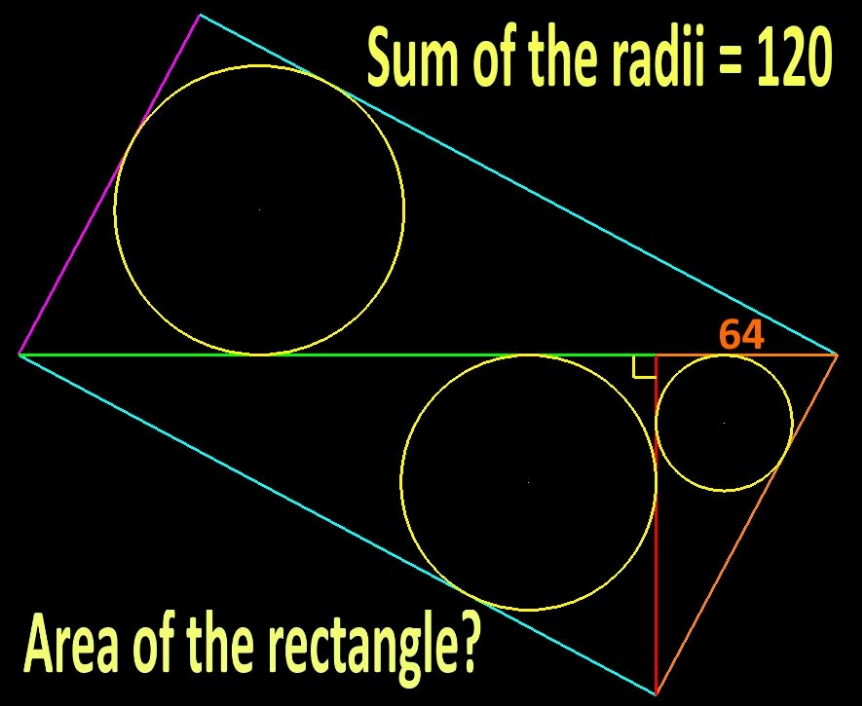
Question Number 185077 by emmanuelson123 last updated on 16/Jan/23
Answered by mahdipoor last updated on 16/Jan/23
![get side of rectangle are A , B Δ1≡Δ2≡Δ3 ⇒ side of Δ1:A , B , (√(A^2 +B^2 )) and r_1 :(1/2)[(A+B)−(√(A^2 +B^2 ))] side of Δ2:((AB)/( (√(A^2 +B^2 )))) , (B^2 /( (√(A^2 +B^3 )))) , B and r_2 :(1/2)[(A+B)−(√(A^2 +B^2 ))]×(B/( (√(A^2 +B^2 )))) side of Δ3:(A^2 /( (√(A^2 +B^2 )))) , ((AB)/( (√(A^2 +B^3 )))) , A and r_2 :(1/2)[(A+B)−(√(A^2 +B^2 ))]×(A/( (√(A^2 +B^2 )))) we know: Σr=120=(1/2)[A+B−(√(A^2 +B^2 ))]×[((A+B)/( (√(A^2 +B^2 ))))+1] =(((A+B)^2 −(A^2 +B^2 ))/(2(√(A^3 +B^2 ))))=((AB)/( (√(A^2 +B^2 )))) and 64=(A^2 /( (√(A^2 +B^2 )))) ⇒⇒B=15(√(289)) A=8(√(289)) ⇒⇒S=AB=15×8×289](https://www.tinkutara.com/question/Q185079.png)
$${get}\:{side}\:{of}\:{rectangle}\:{are}\:{A}\:,\:{B}\: \\ $$$$\Delta\mathrm{1}\equiv\Delta\mathrm{2}\equiv\Delta\mathrm{3}\:\:\:\:\Rightarrow \\ $$$${side}\:{of}\:\Delta\mathrm{1}:{A}\:,\:{B}\:,\:\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} } \\ $$$${and}\:{r}_{\mathrm{1}} :\frac{\mathrm{1}}{\mathrm{2}}\left[\left({A}+{B}\right)−\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }\right] \\ $$$${side}\:{of}\:\Delta\mathrm{2}:\frac{{AB}}{\:\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }}\:,\:\frac{{B}^{\mathrm{2}} }{\:\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{3}} }}\:,\:{B} \\ $$$${and}\:{r}_{\mathrm{2}} :\frac{\mathrm{1}}{\mathrm{2}}\left[\left({A}+{B}\right)−\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }\right]×\frac{{B}}{\:\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }} \\ $$$${side}\:{of}\:\Delta\mathrm{3}:\frac{{A}^{\mathrm{2}} }{\:\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }}\:,\:\frac{{AB}}{\:\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{3}} }}\:,\:{A} \\ $$$${and}\:{r}_{\mathrm{2}} :\frac{\mathrm{1}}{\mathrm{2}}\left[\left({A}+{B}\right)−\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }\right]×\frac{{A}}{\:\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }} \\ $$$${we}\:{know}: \\ $$$$\Sigma{r}=\mathrm{120}=\frac{\mathrm{1}}{\mathrm{2}}\left[{A}+{B}−\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }\right]×\left[\frac{{A}+{B}}{\:\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }}+\mathrm{1}\right] \\ $$$$=\frac{\left({A}+{B}\right)^{\mathrm{2}} −\left({A}^{\mathrm{2}} +{B}^{\mathrm{2}} \right)}{\mathrm{2}\sqrt{{A}^{\mathrm{3}} +{B}^{\mathrm{2}} }}=\frac{{AB}}{\:\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }} \\ $$$${and}\:\:\:\:\mathrm{64}=\frac{{A}^{\mathrm{2}} }{\:\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }} \\ $$$$\Rightarrow\Rightarrow{B}=\mathrm{15}\sqrt{\mathrm{289}}\:\:\:\:\:\:\:{A}=\mathrm{8}\sqrt{\mathrm{289}}\:\:\:\: \\ $$$$\Rightarrow\Rightarrow{S}={AB}=\mathrm{15}×\mathrm{8}×\mathrm{289} \\ $$
