Question Number 185104 by emmanuelson123 last updated on 17/Jan/23

Answered by aba last updated on 17/Jan/23

$$\pi\mathrm{ln}\left(\mathrm{6}+\mathrm{4}\sqrt{\mathrm{2}}\right) \\ $$
Commented by emmanuelson123 last updated on 17/Jan/23
Can you show your work, thank you!
Answered by witcher3 last updated on 24/Jan/23
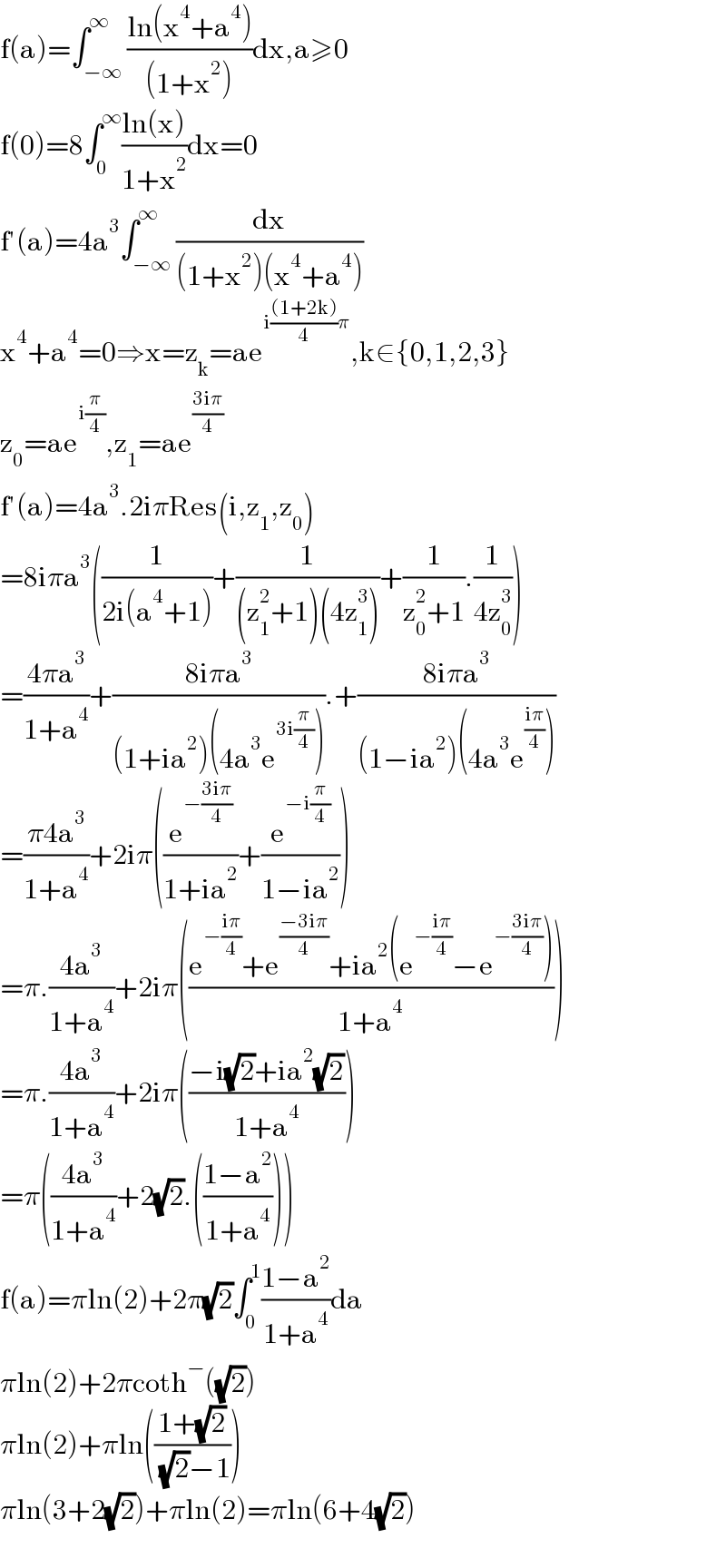
$$\mathrm{f}\left(\mathrm{a}\right)=\int_{−\infty} ^{\infty} \frac{\mathrm{ln}\left(\mathrm{x}^{\mathrm{4}} +\mathrm{a}^{\mathrm{4}} \right)}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\mathrm{dx},\mathrm{a}\geqslant\mathrm{0} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{8}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\mathrm{0} \\ $$$$\mathrm{f}'\left(\mathrm{a}\right)=\mathrm{4a}^{\mathrm{3}} \int_{−\infty} ^{\infty} \frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{4}} +\mathrm{a}^{\mathrm{4}} \right)} \\ $$$$\mathrm{x}^{\mathrm{4}} +\mathrm{a}^{\mathrm{4}} =\mathrm{0}\Rightarrow\mathrm{x}=\mathrm{z}_{\mathrm{k}} =\mathrm{ae}^{\mathrm{i}\frac{\left(\mathrm{1}+\mathrm{2k}\right)}{\mathrm{4}}\pi} ,\mathrm{k}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3}\right\} \\ $$$$\mathrm{z}_{\mathrm{0}} =\mathrm{ae}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} ,\mathrm{z}_{\mathrm{1}} =\mathrm{ae}^{\frac{\mathrm{3i}\pi}{\mathrm{4}}} \\ $$$$\mathrm{f}'\left(\mathrm{a}\right)=\mathrm{4a}^{\mathrm{3}} .\mathrm{2i}\pi\mathrm{Res}\left(\mathrm{i},\mathrm{z}_{\mathrm{1}} ,\mathrm{z}_{\mathrm{0}} \right) \\ $$$$=\mathrm{8i}\pi\mathrm{a}^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2i}\left(\mathrm{a}^{\mathrm{4}} +\mathrm{1}\right)}+\frac{\mathrm{1}}{\left(\mathrm{z}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{4z}_{\mathrm{1}} ^{\mathrm{3}} \right)}+\frac{\mathrm{1}}{\mathrm{z}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{1}}.\frac{\mathrm{1}}{\mathrm{4z}_{\mathrm{0}} ^{\mathrm{3}} }\right) \\ $$$$=\frac{\mathrm{4}\pi\mathrm{a}^{\mathrm{3}} }{\mathrm{1}+\mathrm{a}^{\mathrm{4}} }+\frac{\mathrm{8i}\pi\mathrm{a}^{\mathrm{3}} }{\left(\mathrm{1}+\mathrm{ia}^{\mathrm{2}} \right)\left(\mathrm{4a}^{\mathrm{3}} \mathrm{e}^{\mathrm{3i}\frac{\pi}{\mathrm{4}}} \right)}.+\frac{\mathrm{8i}\pi\mathrm{a}^{\mathrm{3}} }{\left(\mathrm{1}−\mathrm{ia}^{\mathrm{2}} \right)\left(\mathrm{4a}^{\mathrm{3}} \mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)} \\ $$$$=\frac{\pi\mathrm{4a}^{\mathrm{3}} }{\mathrm{1}+\mathrm{a}^{\mathrm{4}} }+\mathrm{2i}\pi\left(\frac{\mathrm{e}^{−\frac{\mathrm{3i}\pi}{\mathrm{4}}} }{\mathrm{1}+\mathrm{ia}^{\mathrm{2}} }+\frac{\mathrm{e}^{−\mathrm{i}\frac{\pi}{\mathrm{4}}} }{\mathrm{1}−\mathrm{ia}^{\mathrm{2}} }\right) \\ $$$$=\pi.\frac{\mathrm{4a}^{\mathrm{3}} }{\mathrm{1}+\mathrm{a}^{\mathrm{4}} }+\mathrm{2i}\pi\left(\frac{\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} +\mathrm{e}^{\frac{−\mathrm{3i}\pi}{\mathrm{4}}} +\mathrm{ia}^{\mathrm{2}} \left(\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} −\mathrm{e}^{−\frac{\mathrm{3i}\pi}{\mathrm{4}}} \right)}{\mathrm{1}+\mathrm{a}^{\mathrm{4}} }\right) \\ $$$$=\pi.\frac{\mathrm{4a}^{\mathrm{3}} }{\mathrm{1}+\mathrm{a}^{\mathrm{4}} }+\mathrm{2i}\pi\left(\frac{−\mathrm{i}\sqrt{\mathrm{2}}+\mathrm{ia}^{\mathrm{2}} \sqrt{\mathrm{2}}}{\mathrm{1}+\mathrm{a}^{\mathrm{4}} }\right) \\ $$$$=\pi\left(\frac{\mathrm{4a}^{\mathrm{3}} }{\mathrm{1}+\mathrm{a}^{\mathrm{4}} }+\mathrm{2}\sqrt{\mathrm{2}}.\left(\frac{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }{\mathrm{1}+\mathrm{a}^{\mathrm{4}} }\right)\right) \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\pi\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{2}\pi\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }{\mathrm{1}+\mathrm{a}^{\mathrm{4}} }\mathrm{da} \\ $$$$\pi\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{2}\pi\mathrm{coth}^{−} \left(\sqrt{\mathrm{2}}\right) \\ $$$$\pi\mathrm{ln}\left(\mathrm{2}\right)+\pi\mathrm{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right) \\ $$$$\pi\mathrm{ln}\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)+\pi\mathrm{ln}\left(\mathrm{2}\right)=\pi\mathrm{ln}\left(\mathrm{6}+\mathrm{4}\sqrt{\mathrm{2}}\right) \\ $$$$ \\ $$
