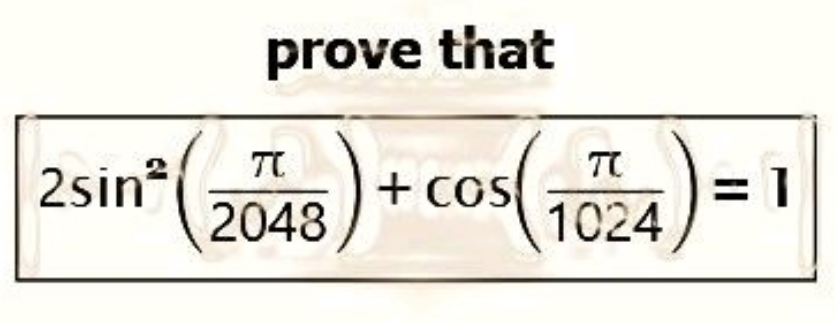
Question Number 185107 by emmanuelson123 last updated on 17/Jan/23
Answered by SEKRET last updated on 17/Jan/23
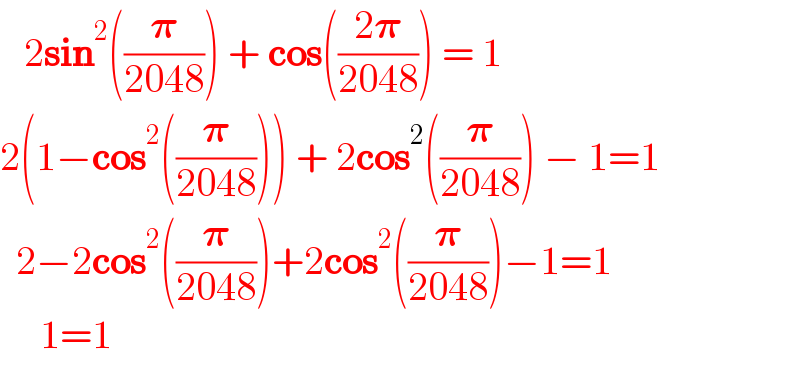
$$\:\:\:\mathrm{2}\boldsymbol{\mathrm{sin}}^{\mathrm{2}} \left(\frac{\boldsymbol{\pi}}{\mathrm{2048}}\right)\:+\:\boldsymbol{\mathrm{cos}}\left(\frac{\mathrm{2}\boldsymbol{\pi}}{\mathrm{2048}}\right)\:=\:\mathrm{1} \\ $$$$\mathrm{2}\left(\mathrm{1}−\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\frac{\boldsymbol{\pi}}{\mathrm{2048}}\right)\right)\:+\:\mathrm{2}\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\frac{\boldsymbol{\pi}}{\mathrm{2048}}\right)\:−\:\mathrm{1}=\mathrm{1} \\ $$$$\:\:\mathrm{2}−\mathrm{2}\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\frac{\boldsymbol{\pi}}{\mathrm{2048}}\right)+\mathrm{2}\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\frac{\boldsymbol{\pi}}{\mathrm{2048}}\right)−\mathrm{1}=\mathrm{1} \\ $$$$\:\:\:\:\:\mathrm{1}=\mathrm{1} \\ $$
Answered by som(math1967) last updated on 17/Jan/23

$${let}\:\frac{\pi}{\mathrm{2048}}=\theta\:\therefore\:\frac{\pi}{\mathrm{1024}}=\mathrm{2}\theta \\ $$$$\therefore\mathrm{2}{sin}^{\mathrm{2}} \theta+{cos}\mathrm{2}\theta \\ $$$$=\mathrm{1}−{cos}\mathrm{2}\theta+{cos}\mathrm{2}\theta \\ $$$$=\mathrm{1} \\ $$
