Question Number 185134 by emmanuelson123 last updated on 17/Jan/23

Answered by som(math1967) last updated on 17/Jan/23
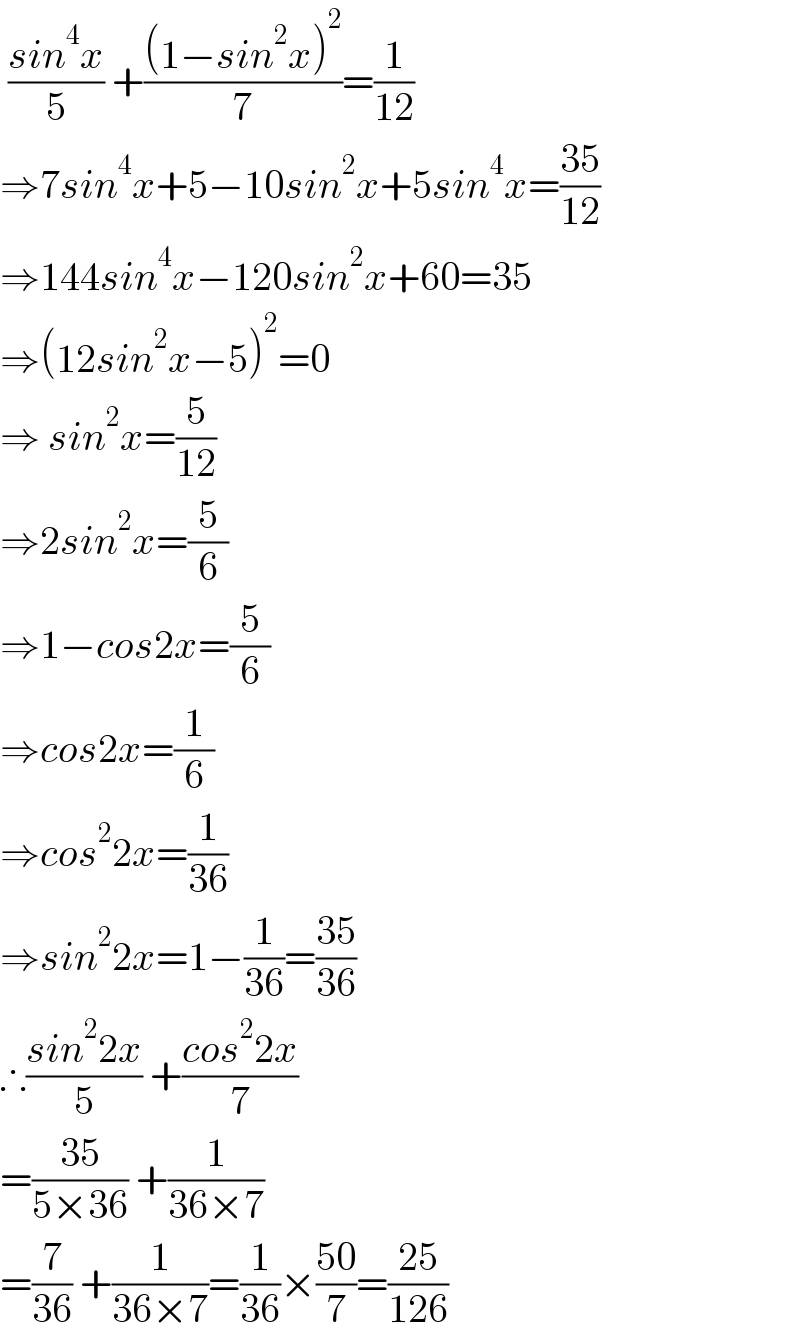
$$\:\frac{{sin}^{\mathrm{4}} {x}}{\mathrm{5}}\:+\frac{\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }{\mathrm{7}}=\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$\Rightarrow\mathrm{7}{sin}^{\mathrm{4}} {x}+\mathrm{5}−\mathrm{10}{sin}^{\mathrm{2}} {x}+\mathrm{5}{sin}^{\mathrm{4}} {x}=\frac{\mathrm{35}}{\mathrm{12}} \\ $$$$\Rightarrow\mathrm{144}{sin}^{\mathrm{4}} {x}−\mathrm{120}{sin}^{\mathrm{2}} {x}+\mathrm{60}=\mathrm{35} \\ $$$$\Rightarrow\left(\mathrm{12}{sin}^{\mathrm{2}} {x}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:{sin}^{\mathrm{2}} {x}=\frac{\mathrm{5}}{\mathrm{12}} \\ $$$$\Rightarrow\mathrm{2}{sin}^{\mathrm{2}} {x}=\frac{\mathrm{5}}{\mathrm{6}} \\ $$$$\Rightarrow\mathrm{1}−{cos}\mathrm{2}{x}=\frac{\mathrm{5}}{\mathrm{6}} \\ $$$$\Rightarrow{cos}\mathrm{2}{x}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\Rightarrow{cos}^{\mathrm{2}} \mathrm{2}{x}=\frac{\mathrm{1}}{\mathrm{36}} \\ $$$$\Rightarrow{sin}^{\mathrm{2}} \mathrm{2}{x}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{36}}=\frac{\mathrm{35}}{\mathrm{36}} \\ $$$$\therefore\frac{{sin}^{\mathrm{2}} \mathrm{2}{x}}{\mathrm{5}}\:+\frac{{cos}^{\mathrm{2}} \mathrm{2}{x}}{\mathrm{7}} \\ $$$$=\frac{\mathrm{35}}{\mathrm{5}×\mathrm{36}}\:+\frac{\mathrm{1}}{\mathrm{36}×\mathrm{7}} \\ $$$$=\frac{\mathrm{7}}{\mathrm{36}}\:+\frac{\mathrm{1}}{\mathrm{36}×\mathrm{7}}=\frac{\mathrm{1}}{\mathrm{36}}×\frac{\mathrm{50}}{\mathrm{7}}=\frac{\mathrm{25}}{\mathrm{126}} \\ $$
