Question Number 185137 by emmanuelson123 last updated on 17/Jan/23
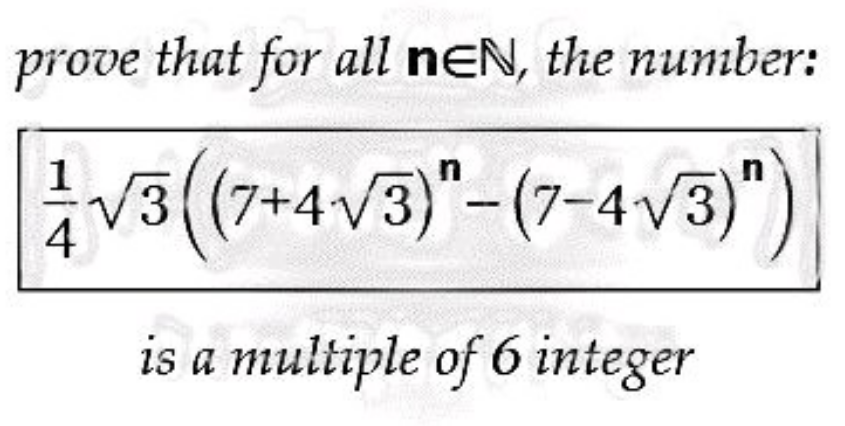
Answered by CElcedricjunior last updated on 17/Jan/23
![montrons que ∀n∈IN ((√3)/4)[(7+4(√3))^n −(7−4(√3))^n ]≡0[6] posons p(n)=((√3)/4)[(7+4(√3))^n −(7−4(√3))^n ] ∗pour n=0 on a ((√3)/4)[(7+4(√3))^0 −(7−4(√3))^0 ]=((√3)/4)(1−1)=0≡0[6] D′ou^� p(0) vrai ∗pour n≥0 supposons p(n) vraie et montrons que p(n+1) l′est aussi au rang (n+1) on a ((√3)/4)[(7+4(√3))^n −(7−4(√3))^n ]≡0[6] =>(((√3)(7+4(√( 3)))^n )/4)≡((√3)/4)(7−4(√3))^n [6] =>(7+4(√3))^n ≡(7−4(√3))^n [6] =>(7+4(√3))^(n+1) ≡(7−4(√3))^(n−1) [6] =>(7+4(√3))^(n+1) −(7−4(√3))^(n−1) ≡0[6] =>((√3)/4)[(7+4(√3))^(n+1) −(7−4(√3))^(n+1) ]≡0[6] cas (7−4(√3))^(n−1) ≤(7−4(√3))^(n+1) d′ou^� p(n+1) vraie donc ∀n∈IN ((√3)/4)[(7+4(√3))^n −(7−4(√3))^n ]≡0[6]](https://www.tinkutara.com/question/Q185145.png)
$$\boldsymbol{{montrons}}\:\boldsymbol{{que}}\:\forall\boldsymbol{{n}}\in\boldsymbol{{IN}} \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left[\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}} −\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}} \right]\equiv\mathrm{0}\left[\mathrm{6}\right] \\ $$$$\boldsymbol{{posons}}\:\boldsymbol{{p}}\left(\boldsymbol{{n}}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left[\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}} −\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}} \right] \\ $$$$\ast\boldsymbol{{pour}}\:\boldsymbol{{n}}=\mathrm{0}\:\boldsymbol{{on}}\:\boldsymbol{{a}}\: \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left[\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right)^{\mathrm{0}} −\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)^{\mathrm{0}} \right]=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left(\mathrm{1}−\mathrm{1}\right)=\mathrm{0}\equiv\mathrm{0}\left[\mathrm{6}\right] \\ $$$$\boldsymbol{{D}}'\boldsymbol{{o}}\grave {\boldsymbol{{u}}}\:{p}\left(\mathrm{0}\right)\:\boldsymbol{{vrai}} \\ $$$$\ast\boldsymbol{{pour}}\:\boldsymbol{{n}}\geqslant\mathrm{0}\:\boldsymbol{{supposons}}\:\boldsymbol{{p}}\left(\boldsymbol{{n}}\right)\:\boldsymbol{{vraie}}\:\boldsymbol{{et}}\:\boldsymbol{{montrons}}\:\boldsymbol{{que}}\:\boldsymbol{{p}}\left(\boldsymbol{{n}}+\mathrm{1}\right)\:\boldsymbol{{l}}'\boldsymbol{{est}}\:\boldsymbol{{aussi}} \\ $$$$\boldsymbol{{au}}\:\boldsymbol{{rang}}\:\left(\boldsymbol{{n}}+\mathrm{1}\right)\:\boldsymbol{{on}}\:\boldsymbol{{a}} \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left[\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}} −\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}} \right]\equiv\mathrm{0}\left[\mathrm{6}\right] \\ $$$$=>\frac{\sqrt{\mathrm{3}}\left(\mathrm{7}+\mathrm{4}\sqrt{\:\mathrm{3}}\right)^{{n}} }{\mathrm{4}}\equiv\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}} \left[\mathrm{6}\right] \\ $$$$=>\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}} \equiv\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}} \left[\mathrm{6}\right] \\ $$$$=>\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}+\mathrm{1}} \equiv\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}−\mathrm{1}} \left[\mathrm{6}\right] \\ $$$$=>\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}+\mathrm{1}} −\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}−\mathrm{1}} \equiv\mathrm{0}\left[\mathrm{6}\right] \\ $$$$=>\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left[\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}+\mathrm{1}} −\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}+\mathrm{1}} \right]\equiv\mathrm{0}\left[\mathrm{6}\right]\:\boldsymbol{{cas}}\:\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}−\mathrm{1}} \leqslant\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}+\mathrm{1}} \\ $$$$\boldsymbol{{d}}'\boldsymbol{{o}}\grave {\boldsymbol{{u}}}\:\boldsymbol{{p}}\left(\boldsymbol{{n}}+\mathrm{1}\right)\:\boldsymbol{{vraie}}\: \\ $$$$\boldsymbol{{donc}}\:\forall\boldsymbol{{n}}\in\boldsymbol{{IN}} \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left[\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\overset{{n}} {\right)}−\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)^{{n}} \right]\equiv\mathrm{0}\left[\mathrm{6}\right] \\ $$$$ \\ $$$$ \\ $$
Commented by aba last updated on 17/Jan/23
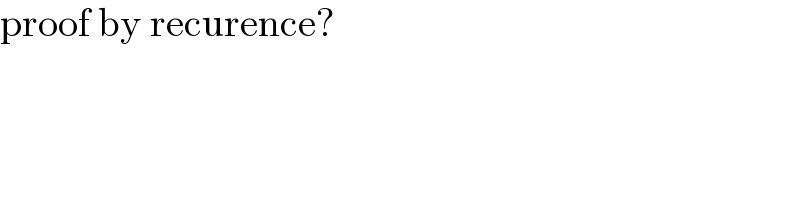
$$\mathrm{proof}\:\mathrm{by}\:\mathrm{recurence}? \\ $$
Answered by JDamian last updated on 17/Jan/23
![S_n =(√3)[(7+4(√3))^n −(7−4(√3))^n ]= =(√3)Σ[C_(n,k) ∙(7^(n−k) ∙(4(√3))^k ] 1≤k≤n k=2p+1 S_n =Σ[C_(n,k) ∙(7^(n−k) ∙(√3)∙(4(√3))^k ] (√3)∙(4(√3))^k =(√3)∙(4(√3))^(2p+1) = =(√3)∙[(4(√3))^2 ]^p ∙4(√3)= =48^p ∙12 S_n =Σ(C_(n,k) ∙7^(n−k) ∙48^p ∙12) (48^p ∙12) mod 6 = 0 ⇒ S_n mod 6 = 0](https://www.tinkutara.com/question/Q185160.png)
$${S}_{{n}} =\sqrt{\mathrm{3}}\left[\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right)^{{n}} −\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)^{{n}} \right]= \\ $$$$=\sqrt{\mathrm{3}}\Sigma\left[{C}_{{n},{k}} \centerdot\left(\mathrm{7}^{{n}−{k}} \centerdot\left(\mathrm{4}\sqrt{\mathrm{3}}\right)^{{k}} \right]\:\:\:\mathrm{1}\leqslant{k}\leqslant{n}\:\:{k}=\mathrm{2}{p}+\mathrm{1}\right. \\ $$$${S}_{{n}} =\Sigma\left[{C}_{{n},{k}} \centerdot\left(\mathrm{7}^{{n}−{k}} \centerdot\sqrt{\mathrm{3}}\centerdot\left(\mathrm{4}\sqrt{\mathrm{3}}\right)^{{k}} \right]\right. \\ $$$$ \\ $$$$\sqrt{\mathrm{3}}\centerdot\left(\mathrm{4}\sqrt{\mathrm{3}}\right)^{{k}} =\sqrt{\mathrm{3}}\centerdot\left(\mathrm{4}\sqrt{\mathrm{3}}\right)^{\mathrm{2}{p}+\mathrm{1}} = \\ $$$$=\sqrt{\mathrm{3}}\centerdot\left[\left(\mathrm{4}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \right]^{{p}} \centerdot\mathrm{4}\sqrt{\mathrm{3}}= \\ $$$$=\mathrm{48}^{{p}} \centerdot\mathrm{12} \\ $$$$ \\ $$$${S}_{{n}} =\Sigma\left({C}_{{n},{k}} \centerdot\mathrm{7}^{{n}−{k}} \centerdot\mathrm{48}^{{p}} \centerdot\mathrm{12}\right) \\ $$$$\left(\mathrm{48}^{{p}} \centerdot\mathrm{12}\right)\:\mathrm{mod}\:\mathrm{6}\:=\:\mathrm{0}\:\:\:\Rightarrow\:\:{S}_{{n}} \mathrm{mod}\:\mathrm{6}\:=\:\mathrm{0} \\ $$
Commented by aba last updated on 17/Jan/23

$$\mathrm{S}_{\mathrm{n}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}…. \\ $$
Commented by aba last updated on 17/Jan/23
![a^n −b^n =(a−b)(Σ_(k=0) ^(n−1) a^k b^(n−1−k) ) S_n =((√3)/4)[8(√3).(Σ_(k=0) ^(n−1) (7+4(√3))^k (7−4(√3))^(n−1−k) )] =6(Σ_(k=0) ^(n−1) ((√3)+2)^(2k) ((√3)−2)^(2(n−1−k)) ) ≡0mod(6)](https://www.tinkutara.com/question/Q185162.png)
$$\:\:\:\mathrm{a}^{\mathrm{n}} −\mathrm{b}^{\mathrm{n}} =\left(\mathrm{a}−\mathrm{b}\right)\left(\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\mathrm{a}^{\mathrm{k}} \mathrm{b}^{\mathrm{n}−\mathrm{1}−\mathrm{k}} \right) \\ $$$$\mathrm{S}_{\mathrm{n}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left[\mathrm{8}\sqrt{\mathrm{3}}.\left(\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right)^{\mathrm{k}} \left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)^{\mathrm{n}−\mathrm{1}−\mathrm{k}} \right)\right] \\ $$$$\:\:\:\:=\mathrm{6}\left(\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\left(\sqrt{\mathrm{3}}+\mathrm{2}\right)^{\mathrm{2k}} \left(\sqrt{\mathrm{3}}−\mathrm{2}\right)^{\mathrm{2}\left(\mathrm{n}−\mathrm{1}−\mathrm{k}\right)} \right) \\ $$$$\:\:\:\equiv\mathrm{0mod}\left(\mathrm{6}\right) \\ $$$$ \\ $$
