Question Number 185166 by Rupesh123 last updated on 17/Jan/23

Answered by mnjuly1970 last updated on 18/Jan/23
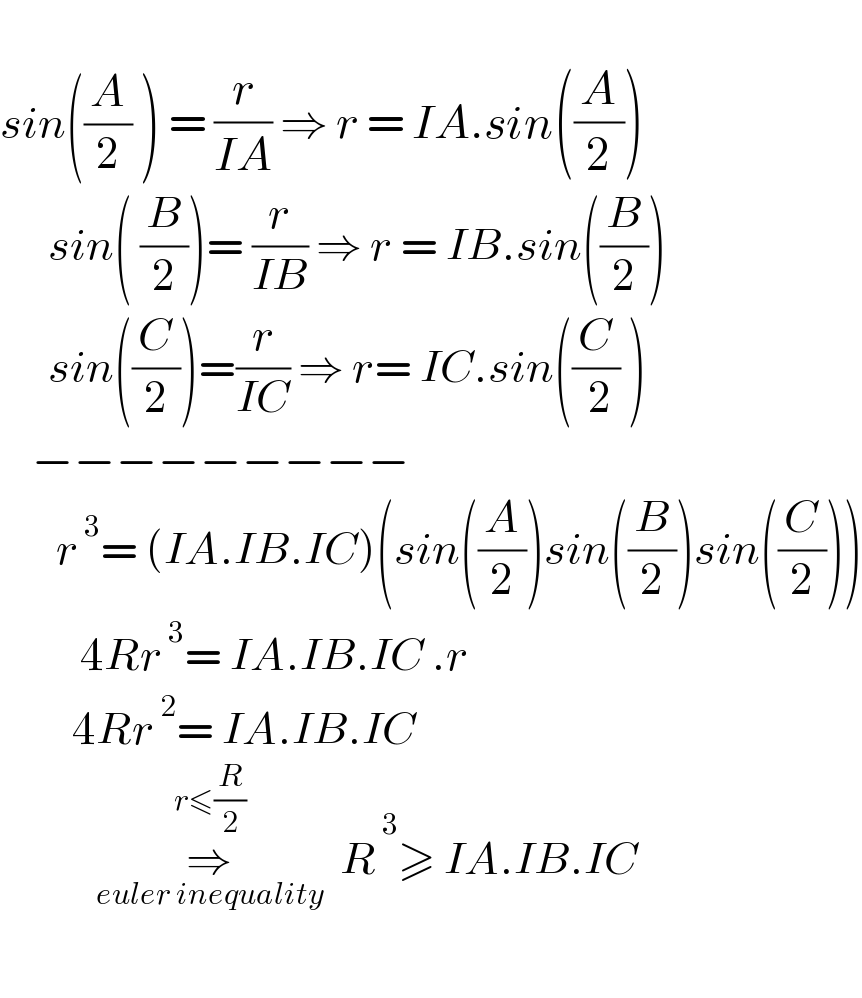
$$\:\: \\ $$$${sin}\left(\frac{{A}}{\mathrm{2}}\:\right)\:=\:\frac{{r}}{{IA}}\:\Rightarrow\:{r}\:=\:{IA}.{sin}\left(\frac{{A}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:{sin}\left(\:\frac{{B}}{\mathrm{2}}\right)=\:\frac{{r}}{{IB}}\:\Rightarrow\:{r}\:=\:{IB}.{sin}\left(\frac{{B}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:{sin}\left(\frac{{C}}{\mathrm{2}}\right)=\frac{{r}}{{IC}}\:\Rightarrow\:{r}=\:{IC}.{sin}\left(\frac{{C}}{\:\mathrm{2}}\:\right) \\ $$$$\:\:\:\:−−−−−−−−− \\ $$$$\:\:\:\:\:\:\:{r}^{\:\mathrm{3}} =\:\left({IA}.{IB}.{IC}\right)\left({sin}\left(\frac{{A}}{\mathrm{2}}\right){sin}\left(\frac{{B}}{\mathrm{2}}\right){sin}\left(\frac{{C}}{\mathrm{2}}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{4}{Rr}^{\:\mathrm{3}} =\:{IA}.{IB}.{IC}\:.{r} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{4}{Rr}^{\:\mathrm{2}} =\:{IA}.{IB}.{IC} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\underset{{euler}\:{inequality}} {\overset{{r}\leqslant\frac{{R}}{\mathrm{2}}} {\Rightarrow}}\:\:{R}^{\:} \overset{\mathrm{3}} {\:}\geqslant\:{IA}.{IB}.{IC} \\ $$$$ \\ $$
