Question Number 185167 by Rupesh123 last updated on 18/Jan/23
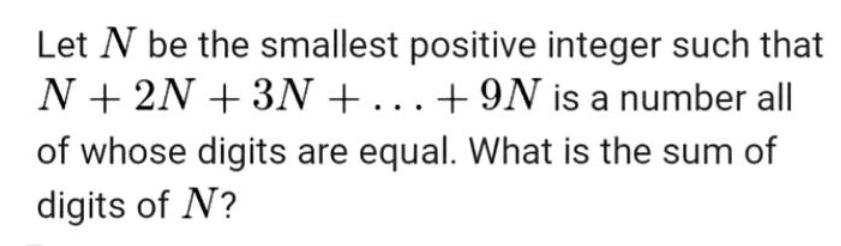
Answered by aba last updated on 18/Jan/23

$$\mathrm{P}=\left(\mathrm{1}+\mathrm{2}+…+\mathrm{9}\right)\mathrm{N}=\mathrm{45N} \\ $$$$\mathrm{if}\:\mathrm{N}\:\mathrm{is}\:\mathrm{an}\:\mathrm{even}\:\mathrm{integer},\:\mathrm{then}\:\mathrm{P}=\mathrm{45N}\:\mathrm{will}\:\mathrm{end}\:\mathrm{in}\:\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{possible}\:\mathrm{as}\:\mathrm{all}\:\mathrm{the}\:\mathrm{digits}\:\mathrm{are}\:\mathrm{same} \\ $$$$\mathrm{if}\:\mathrm{N}\:\mathrm{is}\:\mathrm{an}\:\mathrm{odd}\:\mathrm{integer},\:\mathrm{then}\:\mathrm{P}=\mathrm{45N}\:\mathrm{will}\:\mathrm{end}\:\mathrm{in}\:\mathrm{5} \\ $$$$\mathrm{P}=\mathrm{45N}=\mathrm{555}…\mathrm{55} \\ $$$$\mathrm{also}\:\:\mathrm{as}\:\mathrm{45N}\:\mathrm{is}\:\mathrm{a}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{9} \\ $$$$\mathrm{5}\:\mathrm{must}\:\mathrm{apprear}\:\mathrm{atleast}\:\mathrm{9times} \\ $$$$\mathrm{N}=\frac{\mathrm{555555555}}{\mathrm{45}}=\mathrm{12345679} \\ $$$$\mathrm{Sum}\:\mathrm{of}\:\mathrm{digits}\:\mathrm{of}\:\mathrm{N}=\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{7}+\mathrm{9}=\mathrm{37} \\ $$
