Menu Close

Question-185198

Tinku Tara 0 Comments
Pin




Question Number 185198 by ajfour last updated on 18/Jan/23
Commented by ajfour last updated on 18/Jan/23
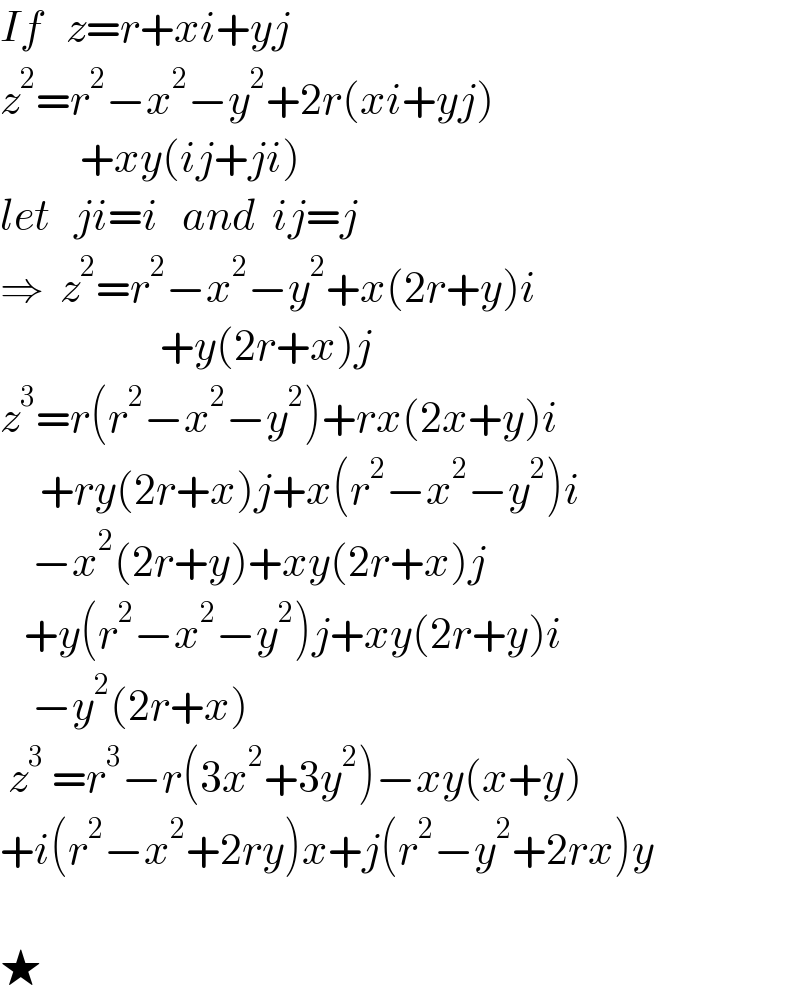
If z=r+xi+yj z^2 =r^2 −x^2 −y^2 +2r(xi+yj) +xy(ij+ji) let ji=i and ij=j ⇒ z^2 =r^2 −x^2 −y^2 +x(2r+y)i +y(2r+x)j z^3 =r(r^2 −x^2 −y^2 )+rx(2x+y)i +ry(2r+x)j+x(r^2 −x^2 −y^2 )i −x^2 (2r+y)+xy(2r+x)j +y(r^2 −x^2 −y^2 )j+xy(2r+y)i −y^2 (2r+x) z^3 =r^3 −r(3x^2 +3y^2 )−xy(x+y) +i(r^2 −x^2 +2ry)x+j(r^2 −y^2 +2rx)y ★
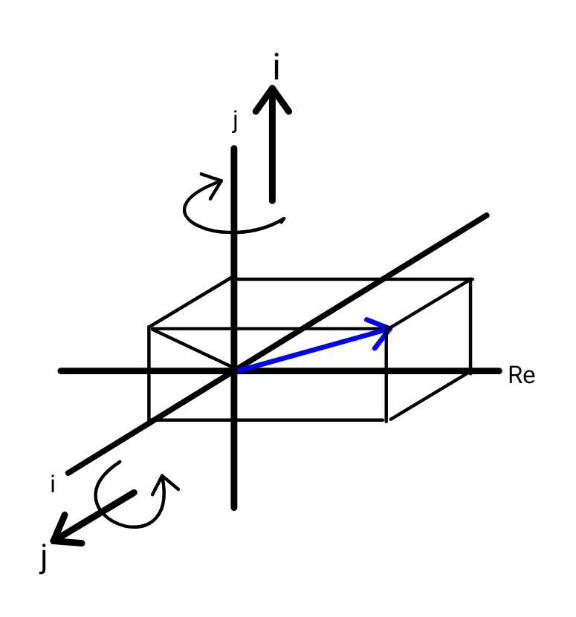
$${If}\:\:\:{z}={r}+{xi}+{yj} \\ $$$${z}^{\mathrm{2}} ={r}^{\mathrm{2}} −{x}^{\mathrm{2}} −{y}^{\mathrm{2}} +\mathrm{2}{r}\left({xi}+{yj}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:+{xy}\left({ij}+{ji}\right) \\ $$$${let}\:\:\:{ji}={i}\:\:\:{and}\:\:{ij}={j} \\ $$$$\Rightarrow\:\:{z}^{\mathrm{2}} ={r}^{\mathrm{2}} −{x}^{\mathrm{2}} −{y}^{\mathrm{2}} +{x}\left(\mathrm{2}{r}+{y}\right){i} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{y}\left(\mathrm{2}{r}+{x}\right){j} \\ $$$${z}^{\mathrm{3}} ={r}\left({r}^{\mathrm{2}} −{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)+{rx}\left(\mathrm{2}{x}+{y}\right){i} \\ $$$$\:\:\:\:\:+{ry}\left(\mathrm{2}{r}+{x}\right){j}+{x}\left({r}^{\mathrm{2}} −{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right){i} \\ $$$$\:\:\:\:−{x}^{\mathrm{2}} \left(\mathrm{2}{r}+{y}\right)+{xy}\left(\mathrm{2}{r}+{x}\right){j} \\ $$$$\:\:\:+{y}\left({r}^{\mathrm{2}} −{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right){j}+{xy}\left(\mathrm{2}{r}+{y}\right){i} \\ $$$$\:\:\:\:−{y}^{\mathrm{2}} \left(\mathrm{2}{r}+{x}\right) \\ $$$$\:{z}^{\mathrm{3}} \:={r}^{\mathrm{3}} −{r}\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} \right)−{xy}\left({x}+{y}\right) \\ $$$$+{i}\left({r}^{\mathrm{2}} −{x}^{\mathrm{2}} +\mathrm{2}{ry}\right){x}+{j}\left({r}^{\mathrm{2}} −{y}^{\mathrm{2}} +\mathrm{2}{rx}\right){y} \\ $$$$ \\ $$$$\bigstar \\ $$
Commented by ajfour last updated on 18/Jan/23
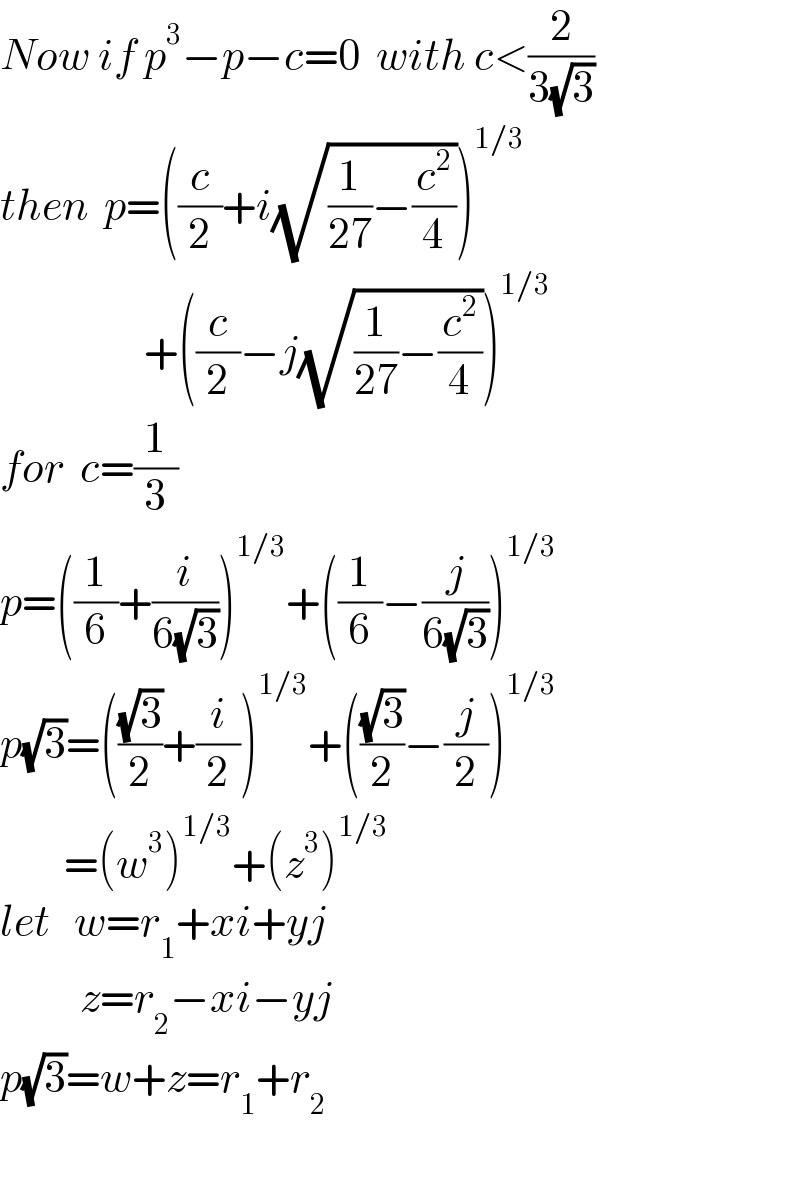
Now if p^3 −p−c=0 with c<(2/(3(√3))) then p=((c/2)+i(√((1/(27))−(c^2 /4))))^(1/3) +((c/2)−j(√((1/(27))−(c^2 /4))))^(1/3) for c=(1/3) p=((1/6)+(i/(6(√3))))^(1/3) +((1/6)−(j/(6(√3))))^(1/3) p(√3)=(((√3)/2)+(i/2))^(1/3) +(((√3)/2)−(j/2))^(1/3) =(w^3 )^(1/3) +(z^3 )^(1/3) let w=r_1 +xi+yj z=r_2 −xi−yj p(√3)=w+z=r_1 +r_2
$${Now}\:{if}\:{p}^{\mathrm{3}} −{p}−{c}=\mathrm{0}\:\:{with}\:{c}<\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$${then}\:\:{p}=\left(\frac{{c}}{\mathrm{2}}+{i}\sqrt{\frac{\mathrm{1}}{\mathrm{27}}−\frac{{c}^{\mathrm{2}} }{\mathrm{4}}}\right)^{\mathrm{1}/\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\frac{{c}}{\mathrm{2}}−{j}\sqrt{\frac{\mathrm{1}}{\mathrm{27}}−\frac{{c}^{\mathrm{2}} }{\mathrm{4}}}\right)^{\mathrm{1}/\mathrm{3}} \\ $$$${for}\:\:{c}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${p}=\left(\frac{\mathrm{1}}{\mathrm{6}}+\frac{{i}}{\mathrm{6}\sqrt{\mathrm{3}}}\right)^{\mathrm{1}/\mathrm{3}} +\left(\frac{\mathrm{1}}{\mathrm{6}}−\frac{{j}}{\mathrm{6}\sqrt{\mathrm{3}}}\right)^{\mathrm{1}/\mathrm{3}} \\ $$$${p}\sqrt{\mathrm{3}}=\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{{i}}{\mathrm{2}}\right)^{\mathrm{1}/\mathrm{3}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{{j}}{\mathrm{2}}\right)^{\mathrm{1}/\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:=\left({w}^{\mathrm{3}} \right)^{\mathrm{1}/\mathrm{3}} +\left({z}^{\mathrm{3}} \right)^{\mathrm{1}/\mathrm{3}} \\ $$$${let}\:\:\:{w}={r}_{\mathrm{1}} +{xi}+{yj} \\ $$$$\:\:\:\:\:\:\:\:\:\:{z}={r}_{\mathrm{2}} −{xi}−{yj} \\ $$$${p}\sqrt{\mathrm{3}}={w}+{z}={r}_{\mathrm{1}} +{r}_{\mathrm{2}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *