Menu Close

Question-185203

Tinku Tara 0 Comments
Pin




Question Number 185203 by KONE last updated on 18/Jan/23
Answered by aba last updated on 18/Jan/23
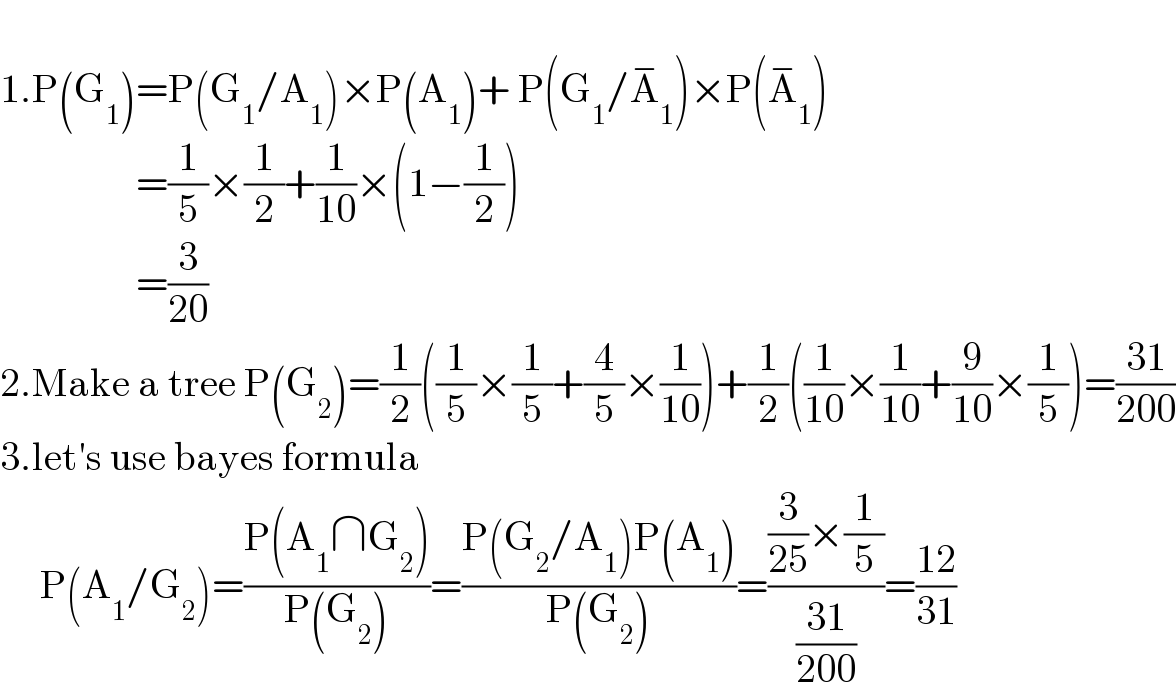
1.P(G_1 )=P(G_1 /A_1 )×P(A_1 )+ P(G_1 /A_1 ^− )×P(A_1 ^− ) =(1/5)×(1/2)+(1/(10))×(1−(1/2)) =(3/(20)) 2.Make a tree P(G_2 )=(1/2)((1/5)×(1/5)+(4/5)×(1/(10)))+(1/2)((1/(10))×(1/(10))+(9/(10))×(1/5))=((31)/(200)) 3.let′s use bayes formula P(A_1 /G_2 )=((P(A_1 ∩G_2 ))/(P(G_2 )))=((P(G_2 /A_1 )P(A_1 ))/(P(G_2 )))=(((3/(25))×(1/5))/((31)/(200)))=((12)/(31))
$$ \\ $$$$\mathrm{1}.\mathrm{P}\left(\mathrm{G}_{\mathrm{1}} \right)=\mathrm{P}\left(\mathrm{G}_{\mathrm{1}} /\mathrm{A}_{\mathrm{1}} \right)×\mathrm{P}\left(\mathrm{A}_{\mathrm{1}} \right)+\:\mathrm{P}\left(\mathrm{G}_{\mathrm{1}} /\overset{−} {\mathrm{A}}_{\mathrm{1}} \right)×\mathrm{P}\left(\overset{−} {\mathrm{A}}_{\mathrm{1}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{5}}×\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{10}}×\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}}{\mathrm{20}} \\ $$$$\mathrm{2}.\mathrm{Make}\:\mathrm{a}\:\mathrm{tree}\:\mathrm{P}\left(\mathrm{G}_{\mathrm{2}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{5}}×\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{4}}{\mathrm{5}}×\frac{\mathrm{1}}{\mathrm{10}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{10}}×\frac{\mathrm{1}}{\mathrm{10}}+\frac{\mathrm{9}}{\mathrm{10}}×\frac{\mathrm{1}}{\mathrm{5}}\right)=\frac{\mathrm{31}}{\mathrm{200}} \\ $$$$\mathrm{3}.\mathrm{let}'\mathrm{s}\:\mathrm{use}\:\mathrm{bayes}\:\mathrm{formula} \\ $$$$\:\:\:\:\:\mathrm{P}\left(\mathrm{A}_{\mathrm{1}} /\mathrm{G}_{\mathrm{2}} \right)=\frac{\mathrm{P}\left(\mathrm{A}_{\mathrm{1}} \cap\mathrm{G}_{\mathrm{2}} \right)}{\mathrm{P}\left(\mathrm{G}_{\mathrm{2}} \right)}=\frac{\mathrm{P}\left(\mathrm{G}_{\mathrm{2}} /\mathrm{A}_{\mathrm{1}} \right)\mathrm{P}\left(\mathrm{A}_{\mathrm{1}} \right)}{\mathrm{P}\left(\mathrm{G}_{\mathrm{2}} \right)}=\frac{\frac{\mathrm{3}}{\mathrm{25}}×\frac{\mathrm{1}}{\mathrm{5}}}{\frac{\mathrm{31}}{\mathrm{200}}}=\frac{\mathrm{12}}{\mathrm{31}} \\ $$
Answered by aba last updated on 18/Jan/23
4.1 P(G_k )=P(G_k /A_k )×P(A_k )+P(G_k /A_k ^− )×P(A_k ^− ) =(1/5)P(A_k )+(1/(10))(1−P(A_k )) =(1/(10))(1+P(A_k )) 4.2 P(A_(k+1) )=P(G_k ∩A_k )+P(G_k ^− ∩A_k ^− ) =P(G_k /A_k )×P(A_k )+P(G_k ^− /A_k ^− )×P(A_k ^− ) =(1/5)P(A_k )+(9/(10))(1−P(A_k )) =(9/(10))−(7/(10))P(A_k ) 4.3 geometric arithmetic sequence (U_(n+1) =aU_n +b) let l=(9/(10))−(7/(10))l ⇒ l=(9/(17)) v_k =P(A_k )−(9/(17)) ⇒ v_(k+1) =((−7)/(10))v_k ⇒ v_k =(((−7)/(10)))^(k−1) v_1 P(A_k )=(−(7/(10)))^(k−1) (P(A_1 )−(9/(17)))+(9/(17)) =−(1/(34))(−(7/(10)))^(k−1) +(9/(17)) we then deduce : P(G_k )=((13)/(85))−(1/(340))(−(7/(10)))^(k−1)
$$\mathrm{4}.\mathrm{1}\:\mathrm{P}\left(\mathrm{G}_{\mathrm{k}} \right)=\mathrm{P}\left(\mathrm{G}_{\mathrm{k}} /\mathrm{A}_{\mathrm{k}} \right)×\mathrm{P}\left(\mathrm{A}_{\mathrm{k}} \right)+\mathrm{P}\left(\mathrm{G}_{\mathrm{k}} /\overset{−} {\mathrm{A}}_{\mathrm{k}} \right)×\mathrm{P}\left(\overset{−} {\mathrm{A}}_{\mathrm{k}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{P}\left(\mathrm{A}_{\mathrm{k}} \right)+\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{1}−\mathrm{P}\left(\mathrm{A}_{\mathrm{k}} \right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{1}+\mathrm{P}\left(\mathrm{A}_{\mathrm{k}} \right)\right) \\ $$$$\:\mathrm{4}.\mathrm{2}\:\:\mathrm{P}\left(\mathrm{A}_{\mathrm{k}+\mathrm{1}} \right)=\mathrm{P}\left(\mathrm{G}_{\mathrm{k}} \cap\mathrm{A}_{\mathrm{k}} \right)+\mathrm{P}\left(\overset{−} {\mathrm{G}}_{\mathrm{k}} \cap\overset{−} {\mathrm{A}}_{\mathrm{k}} \right)\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{P}\left(\mathrm{G}_{\mathrm{k}} /\mathrm{A}_{\mathrm{k}} \right)×\mathrm{P}\left(\mathrm{A}_{\mathrm{k}} \right)+\mathrm{P}\left(\overset{−} {\mathrm{G}}_{\mathrm{k}} /\overset{−} {\mathrm{A}}_{\mathrm{k}} \right)×\mathrm{P}\left(\overset{−} {\mathrm{A}}_{\mathrm{k}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{P}\left(\mathrm{A}_{\mathrm{k}} \right)+\frac{\mathrm{9}}{\mathrm{10}}\left(\mathrm{1}−\mathrm{P}\left(\mathrm{A}_{\mathrm{k}} \right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{9}}{\mathrm{10}}−\frac{\mathrm{7}}{\mathrm{10}}\mathrm{P}\left(\mathrm{A}_{\mathrm{k}} \right) \\ $$$$\mathrm{4}.\mathrm{3}\:\mathrm{geometric}\:\mathrm{arithmetic}\:\mathrm{sequence}\:\left(\mathrm{U}_{\mathrm{n}+\mathrm{1}} =\mathrm{aU}_{\mathrm{n}} +\mathrm{b}\right) \\ $$$$\:\mathrm{let}\:\mathrm{l}=\frac{\mathrm{9}}{\mathrm{10}}−\frac{\mathrm{7}}{\mathrm{10}}\mathrm{l}\:\Rightarrow\:\mathrm{l}=\frac{\mathrm{9}}{\mathrm{17}} \\ $$$$\mathrm{v}_{\mathrm{k}} =\mathrm{P}\left(\mathrm{A}_{\mathrm{k}} \right)−\frac{\mathrm{9}}{\mathrm{17}}\:\:\Rightarrow\:\mathrm{v}_{\mathrm{k}+\mathrm{1}} =\frac{−\mathrm{7}}{\mathrm{10}}\mathrm{v}_{\mathrm{k}} \\ $$$$\:\Rightarrow\:\mathrm{v}_{\mathrm{k}} =\left(\frac{−\mathrm{7}}{\mathrm{10}}\right)^{\mathrm{k}−\mathrm{1}} \mathrm{v}_{\mathrm{1}} \\ $$$$\mathrm{P}\left(\mathrm{A}_{\mathrm{k}} \right)=\left(−\frac{\mathrm{7}}{\mathrm{10}}\right)^{\mathrm{k}−\mathrm{1}} \left(\mathrm{P}\left(\mathrm{A}_{\mathrm{1}} \right)−\frac{\mathrm{9}}{\mathrm{17}}\right)+\frac{\mathrm{9}}{\mathrm{17}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{34}}\left(−\frac{\mathrm{7}}{\mathrm{10}}\right)^{\mathrm{k}−\mathrm{1}} +\frac{\mathrm{9}}{\mathrm{17}} \\ $$$$\mathrm{we}\:\mathrm{then}\:\mathrm{deduce}\:: \\ $$$$\mathrm{P}\left(\mathrm{G}_{\mathrm{k}} \right)=\frac{\mathrm{13}}{\mathrm{85}}−\frac{\mathrm{1}}{\mathrm{340}}\left(−\frac{\mathrm{7}}{\mathrm{10}}\right)^{\mathrm{k}−\mathrm{1}} \\ $$
Commented by KONE last updated on 20/Jan/23
thank you sir
$${thank}\:{you}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *