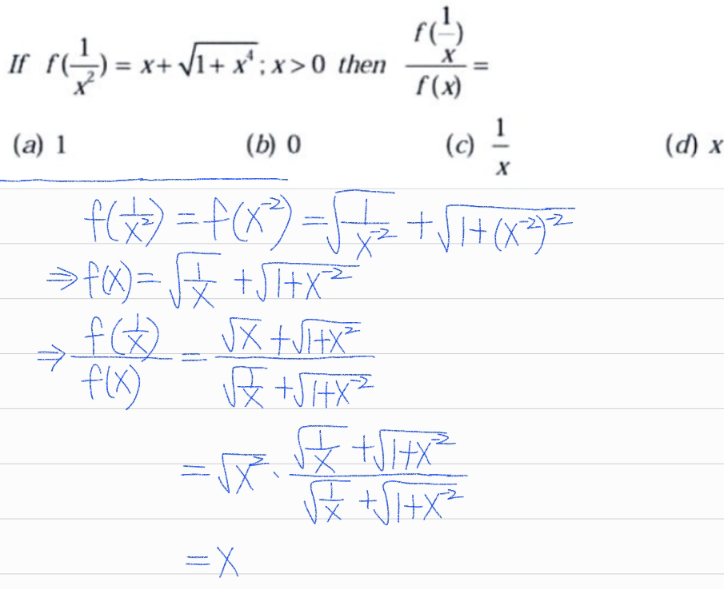Question Number 185211 by Rupesh123 last updated on 18/Jan/23
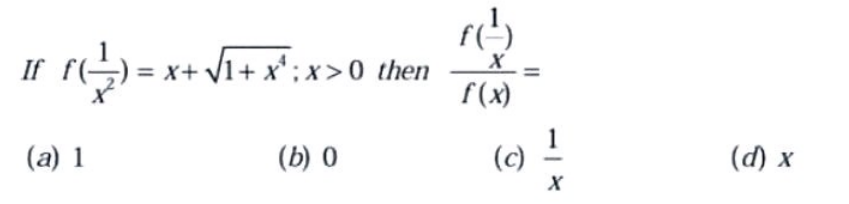
Answered by manolex last updated on 18/Jan/23

$${x} \\ $$$$ \\ $$
Answered by manolex last updated on 18/Jan/23
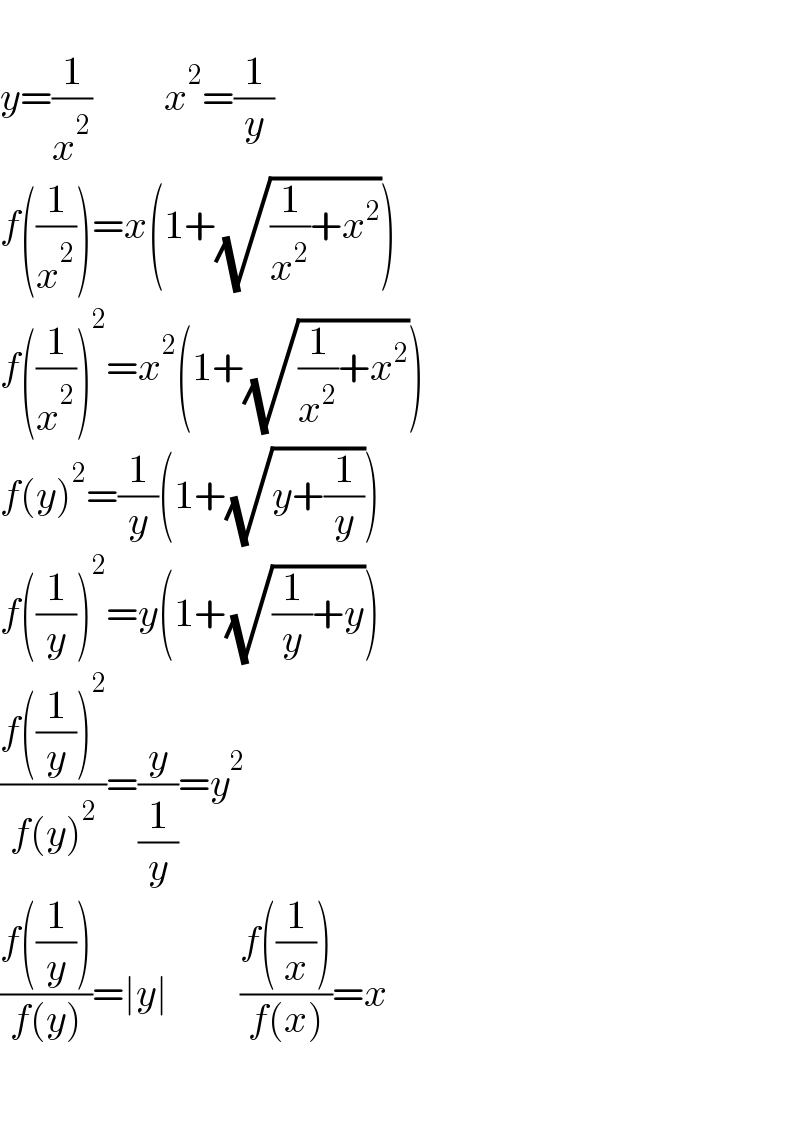
$$ \\ $$$${y}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} =\frac{\mathrm{1}}{{y}} \\ $$$${f}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)={x}\left(\mathrm{1}+\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+{x}^{\mathrm{2}} }\right) \\ $$$${f}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} ={x}^{\mathrm{2}} \left(\mathrm{1}+\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+{x}^{\mathrm{2}} }\right) \\ $$$${f}\left({y}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{{y}}\left(\mathrm{1}+\sqrt{{y}+\frac{\mathrm{1}}{{y}}}\right) \\ $$$${f}\left(\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} ={y}\left(\mathrm{1}+\sqrt{\frac{\mathrm{1}}{{y}}+{y}}\right) \\ $$$$\frac{{f}\left(\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} }{{f}\left({y}\right)^{\mathrm{2}} }=\frac{{y}}{\frac{\mathrm{1}}{{y}}}={y}^{\mathrm{2}} \\ $$$$\frac{{f}\left(\frac{\mathrm{1}}{{y}}\right)}{{f}\left({y}\right)}=\mid{y}\mid\:\:\:\:\:\:\:\:\:\frac{{f}\left(\frac{\mathrm{1}}{{x}}\right)}{{f}\left({x}\right)}={x} \\ $$$$ \\ $$$$ \\ $$
Commented by JDamian last updated on 19/Jan/23
Are you sure 3rd line is right?
Answered by 123564 last updated on 20/Jan/23