Question Number 185270 by Mingma last updated on 19/Jan/23

Answered by mr W last updated on 20/Jan/23
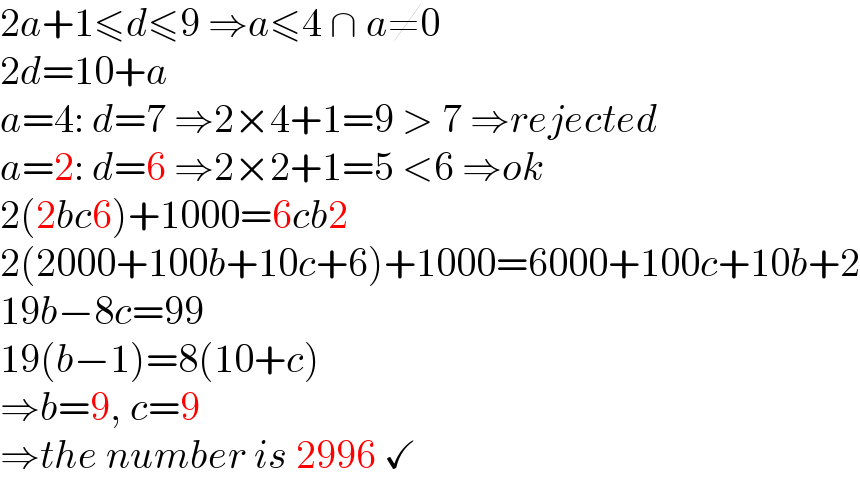
$$\mathrm{2}{a}+\mathrm{1}\leqslant{d}\leqslant\mathrm{9}\:\Rightarrow{a}\leqslant\mathrm{4}\:\cap\:{a}\neq\mathrm{0} \\ $$$$\mathrm{2}{d}=\mathrm{10}+{a} \\ $$$${a}=\mathrm{4}:\:{d}=\mathrm{7}\:\Rightarrow\mathrm{2}×\mathrm{4}+\mathrm{1}=\mathrm{9}\:>\:\mathrm{7}\:\Rightarrow{rejected} \\ $$$${a}=\mathrm{2}:\:{d}=\mathrm{6}\:\Rightarrow\mathrm{2}×\mathrm{2}+\mathrm{1}=\mathrm{5}\:<\mathrm{6}\:\Rightarrow{ok} \\ $$$$\mathrm{2}\left(\mathrm{2}{bc}\mathrm{6}\right)+\mathrm{1000}=\mathrm{6}{cb}\mathrm{2} \\ $$$$\mathrm{2}\left(\mathrm{2000}+\mathrm{100}{b}+\mathrm{10}{c}+\mathrm{6}\right)+\mathrm{1000}=\mathrm{6000}+\mathrm{100}{c}+\mathrm{10}{b}+\mathrm{2} \\ $$$$\mathrm{19}{b}−\mathrm{8}{c}=\mathrm{99} \\ $$$$\mathrm{19}\left({b}−\mathrm{1}\right)=\mathrm{8}\left(\mathrm{10}+{c}\right) \\ $$$$\Rightarrow{b}=\mathrm{9},\:{c}=\mathrm{9} \\ $$$$\Rightarrow{the}\:{number}\:{is}\:\mathrm{2996}\:\checkmark \\ $$
Commented by Rasheed.Sindhi last updated on 21/Jan/23

$${e}^{{x}} {cellent}\:\boldsymbol{{sir}}! \\ $$
