Question Number 185284 by Mingma last updated on 19/Jan/23
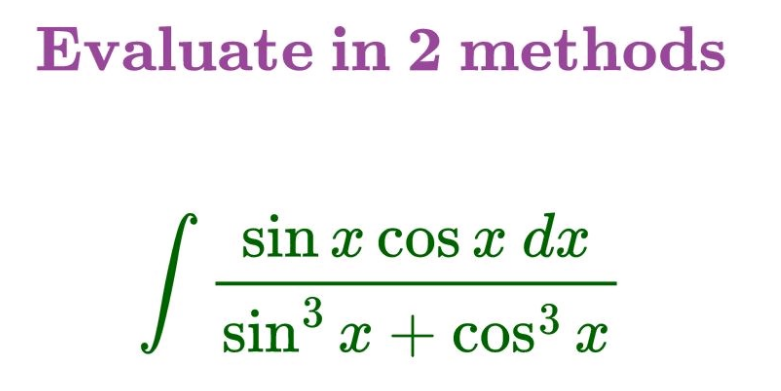
Answered by MJS_new last updated on 20/Jan/23
![one method: ∫((sin x cos x)/(sin^3 x +cos^3 x))dx= [t=cos (x+(π/4)) → dx=−(dt/(sin (x+(π/4))))] =−((√2)/2)∫((2t^2 −1)/((t−1)(t+1)(2t^2 +1)))dt= =((√2)/(12))∫(dt/(t+1))−((√2)/(12))∫(dt/(t−1))−((2(√2))/3)∫(dt/(2t^2 +1))= =((√2)/(12))ln (t+1) −((√2)/(12))ln (t−1) −(2/3)arctan (√2)t = =((√2)/(12))ln ∣((sin x −cos x −(√2))/(sin x +cos x +(√2)))∣ +(2/3)arctan (sin x −cos x) +C](https://www.tinkutara.com/question/Q185377.png)
$$\mathrm{one}\:\mathrm{method}: \\ $$$$\int\frac{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}{\mathrm{sin}^{\mathrm{3}} \:{x}\:+\mathrm{cos}^{\mathrm{3}} \:{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)\:\rightarrow\:{dx}=−\frac{{dt}}{\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)}\right] \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}}{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)\left(\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}\right)}{dt}= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{12}}\int\frac{{dt}}{{t}+\mathrm{1}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{12}}\int\frac{{dt}}{{t}−\mathrm{1}}−\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\int\frac{{dt}}{\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{12}}\mathrm{ln}\:\left({t}+\mathrm{1}\right)\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{12}}\mathrm{ln}\:\left({t}−\mathrm{1}\right)\:−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arctan}\:\sqrt{\mathrm{2}}{t}\:= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{12}}\mathrm{ln}\:\mid\frac{\mathrm{sin}\:{x}\:−\mathrm{cos}\:{x}\:−\sqrt{\mathrm{2}}}{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}\:+\sqrt{\mathrm{2}}}\mid\:+\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arctan}\:\left(\mathrm{sin}\:{x}\:−\mathrm{cos}\:{x}\right)\:+{C} \\ $$
