Question Number 185310 by mathlove last updated on 20/Jan/23

Commented by HeferH last updated on 20/Jan/23

$${suma}\:{de}\:{sumas}?\: \\ $$
Answered by Rasheed.Sindhi last updated on 20/Jan/23
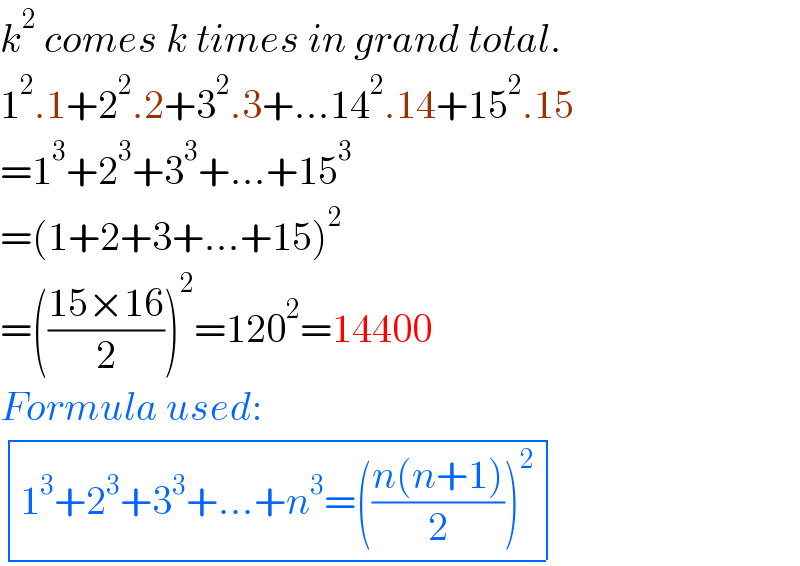
$${k}^{\mathrm{2}} \:{comes}\:{k}\:{times}\:{in}\:{grand}\:{total}. \\ $$$$\mathrm{1}^{\mathrm{2}} .\mathrm{1}+\mathrm{2}^{\mathrm{2}} .\mathrm{2}+\mathrm{3}^{\mathrm{2}} .\mathrm{3}+…\mathrm{14}^{\mathrm{2}} .\mathrm{14}+\mathrm{15}^{\mathrm{2}} .\mathrm{15} \\ $$$$=\mathrm{1}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} +\mathrm{3}^{\mathrm{3}} +…+\mathrm{15}^{\mathrm{3}} \\ $$$$=\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+…+\mathrm{15}\right)^{\mathrm{2}} \\ $$$$=\left(\frac{\mathrm{15}×\mathrm{16}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{120}^{\mathrm{2}} =\mathrm{14400} \\ $$$${Formula}\:{used}: \\ $$$$\begin{array}{|c|}{\mathrm{1}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} +\mathrm{3}^{\mathrm{3}} +…+{n}^{\mathrm{3}} =\left(\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\right)^{\mathrm{2}} }\\\hline\end{array} \\ $$
