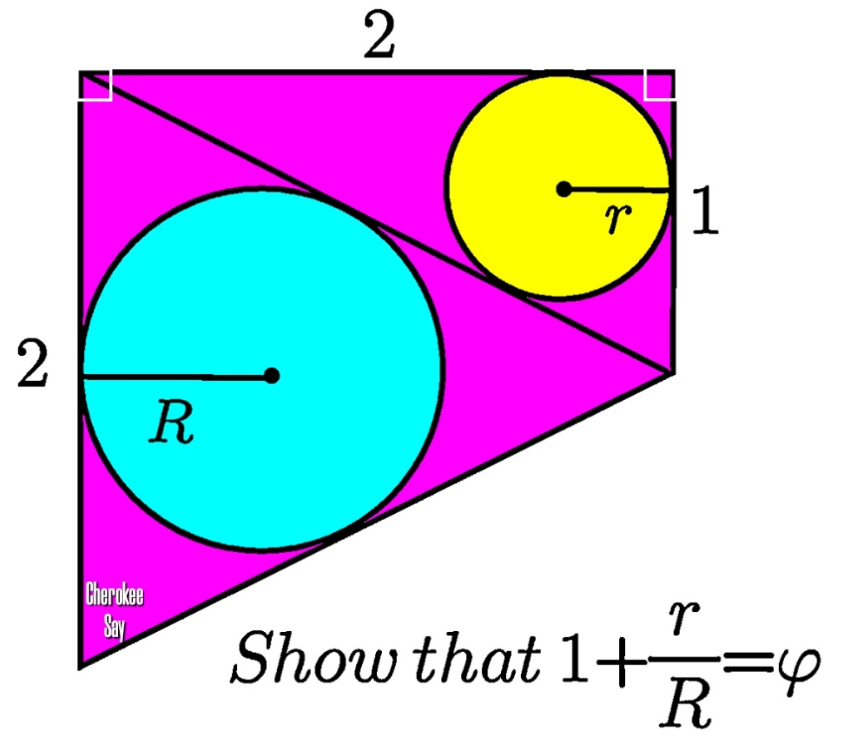
Question Number 185324 by cherokeesay last updated on 20/Jan/23
Answered by som(math1967) last updated on 20/Jan/23
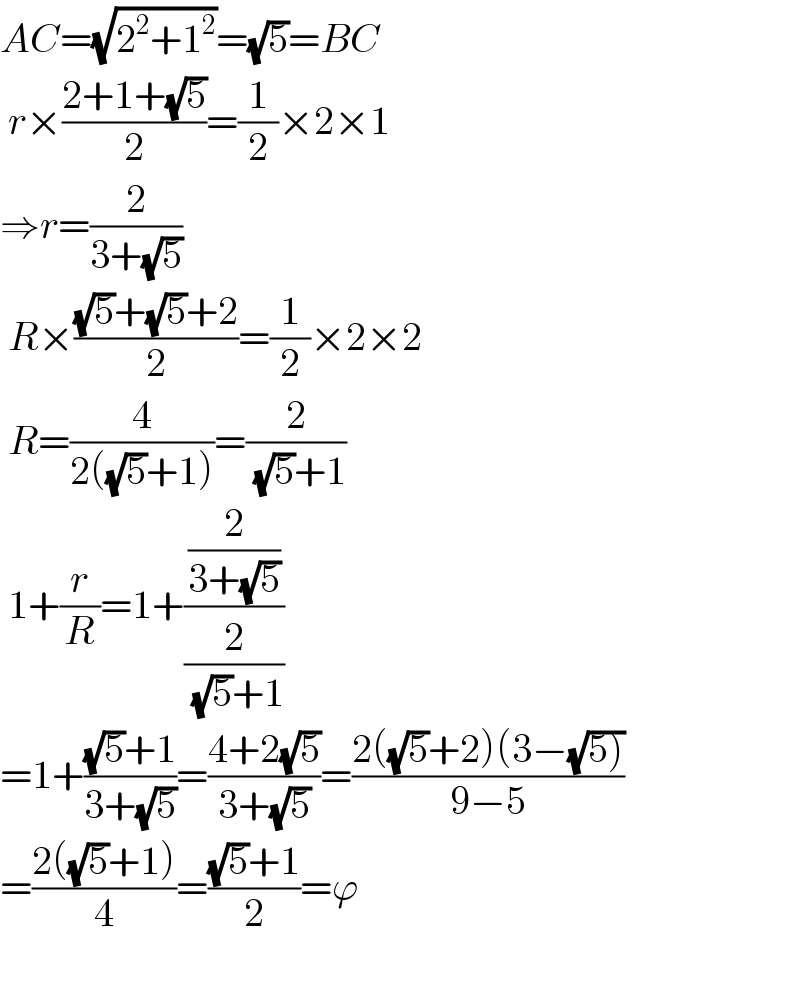
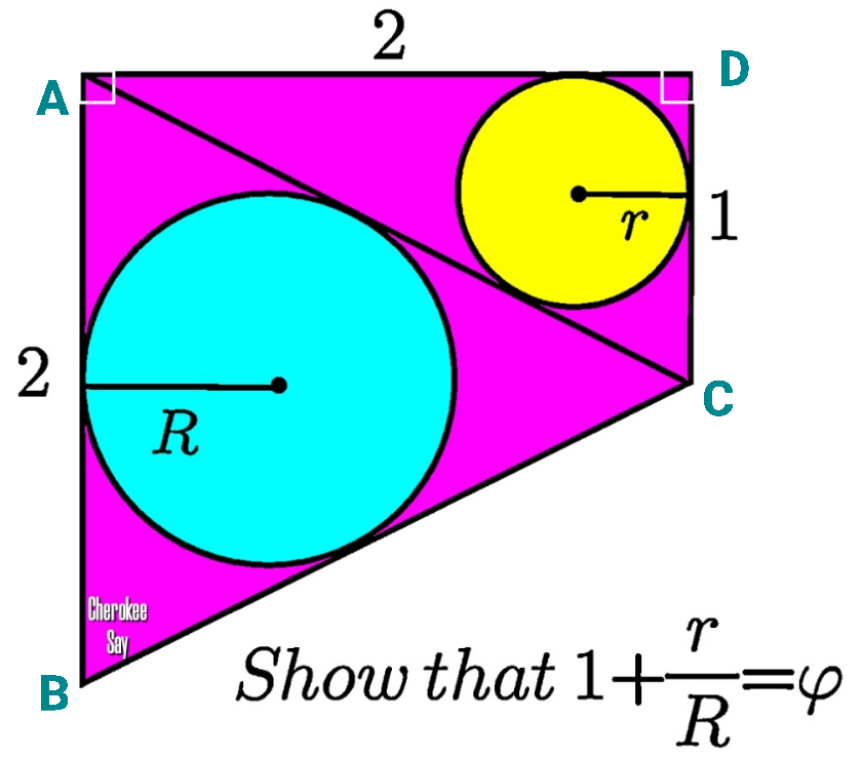
$${AC}=\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }=\sqrt{\mathrm{5}}={BC} \\ $$$$\:{r}×\frac{\mathrm{2}+\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}×\mathrm{1} \\ $$$$\Rightarrow{r}=\frac{\mathrm{2}}{\mathrm{3}+\sqrt{\mathrm{5}}} \\ $$$$\:{R}×\frac{\sqrt{\mathrm{5}}+\sqrt{\mathrm{5}}+\mathrm{2}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}×\mathrm{2} \\ $$$$\:{R}=\frac{\mathrm{4}}{\mathrm{2}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}+\mathrm{1}} \\ $$$$\:\mathrm{1}+\frac{{r}}{{R}}=\mathrm{1}+\frac{\frac{\mathrm{2}}{\mathrm{3}+\sqrt{\mathrm{5}}}}{\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}+\mathrm{1}}} \\ $$$$=\mathrm{1}+\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{3}+\sqrt{\mathrm{5}}}=\frac{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{3}+\sqrt{\mathrm{5}}}=\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}+\mathrm{2}\right)\left(\mathrm{3}−\sqrt{\left.\mathrm{5}\right)}\right.}{\mathrm{9}−\mathrm{5}} \\ $$$$=\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)}{\mathrm{4}}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}=\varphi \\ $$$$ \\ $$
Commented by som(math1967) last updated on 20/Jan/23
Commented by cherokeesay last updated on 20/Jan/23

$${Nice}\:!\:{thank}\:{you}. \\ $$
