Question Number 185325 by Ml last updated on 20/Jan/23

Answered by aleks041103 last updated on 20/Jan/23
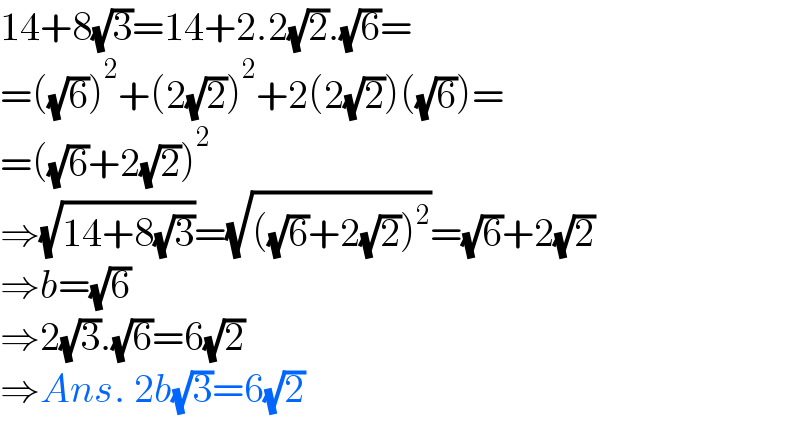
$$\mathrm{14}+\mathrm{8}\sqrt{\mathrm{3}}=\mathrm{14}+\mathrm{2}.\mathrm{2}\sqrt{\mathrm{2}}.\sqrt{\mathrm{6}}= \\ $$$$=\left(\sqrt{\mathrm{6}}\right)^{\mathrm{2}} +\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)\left(\sqrt{\mathrm{6}}\right)= \\ $$$$=\left(\sqrt{\mathrm{6}}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\sqrt{\mathrm{14}+\mathrm{8}\sqrt{\mathrm{3}}}=\sqrt{\left(\sqrt{\mathrm{6}}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }=\sqrt{\mathrm{6}}+\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{b}=\sqrt{\mathrm{6}} \\ $$$$\Rightarrow\mathrm{2}\sqrt{\mathrm{3}}.\sqrt{\mathrm{6}}=\mathrm{6}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{Ans}.\:\mathrm{2}{b}\sqrt{\mathrm{3}}=\mathrm{6}\sqrt{\mathrm{2}} \\ $$
Answered by HeferH last updated on 20/Jan/23
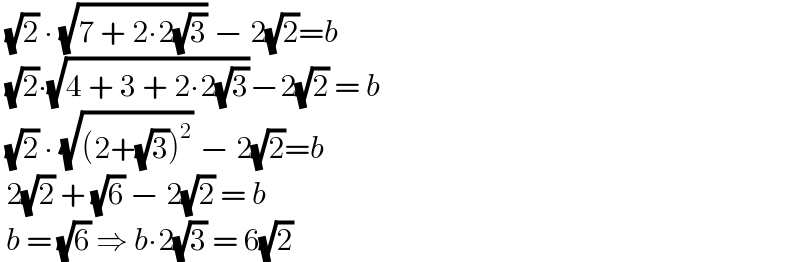
$$\:\sqrt{\mathrm{2}}\:\centerdot\:\sqrt{\mathrm{7}\:+\:\mathrm{2}\centerdot\mathrm{2}\sqrt{\mathrm{3}}}\:−\:\mathrm{2}\sqrt{\mathrm{2}}={b} \\ $$$$\:\sqrt{\mathrm{2}}\centerdot\sqrt{\mathrm{4}\:+\:\mathrm{3}\:+\:\mathrm{2}\centerdot\mathrm{2}\sqrt{\mathrm{3}}}−\mathrm{2}\sqrt{\mathrm{2}}\:=\:{b} \\ $$$$\:\sqrt{\mathrm{2}}\:\centerdot\:\sqrt{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\:−\:\mathrm{2}\sqrt{\mathrm{2}}={b} \\ $$$$\:\mathrm{2}\sqrt{\mathrm{2}}\:+\:\sqrt{\mathrm{6}}\:−\:\mathrm{2}\sqrt{\mathrm{2}}\:=\:{b} \\ $$$$\:{b}\:=\:\sqrt{\mathrm{6}}\:\Rightarrow\:{b}\centerdot\mathrm{2}\sqrt{\mathrm{3}}\:=\:\mathrm{6}\sqrt{\mathrm{2}} \\ $$
