Question Number 185387 by Rupesh123 last updated on 20/Jan/23
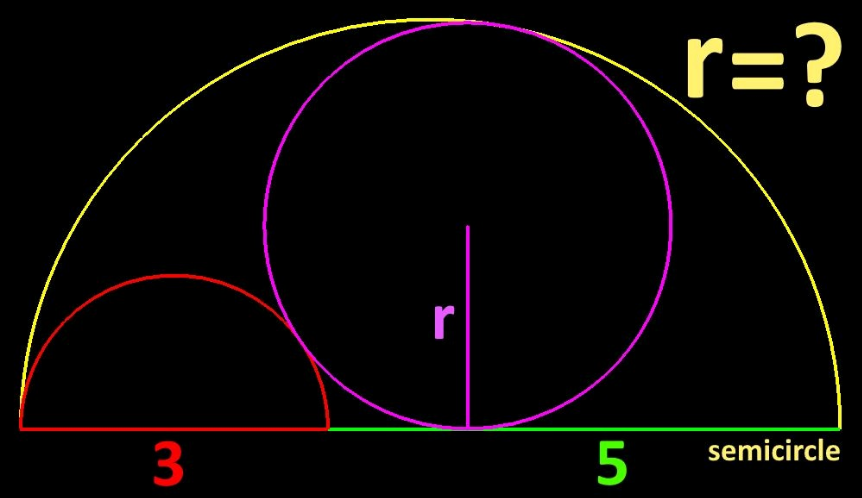
Answered by HeferH last updated on 21/Jan/23
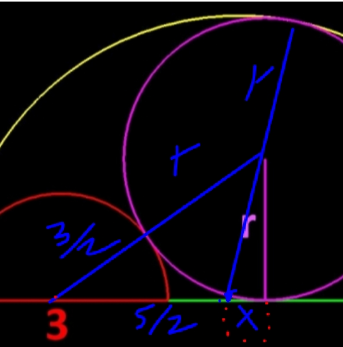
Commented by HeferH last updated on 21/Jan/23
![x = (√((4−r)^2 −r^2 )) ⇒ [(√((4−r)^2 −r^2 )) + (5/2)]^2 + r^2 = ((3/2) + r)^2 r = ((240)/(121))](https://www.tinkutara.com/question/Q185392.png)
$${x}\:=\:\sqrt{\left(\mathrm{4}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\:\left[\sqrt{\left(\mathrm{4}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }\:+\:\frac{\mathrm{5}}{\mathrm{2}}\right]^{\mathrm{2}} +\:{r}^{\mathrm{2}} \:=\:\left(\frac{\mathrm{3}}{\mathrm{2}}\:+\:{r}\right)^{\mathrm{2}} \\ $$$$\:{r}\:=\:\frac{\mathrm{240}}{\mathrm{121}}\: \\ $$
Answered by mr W last updated on 21/Jan/23
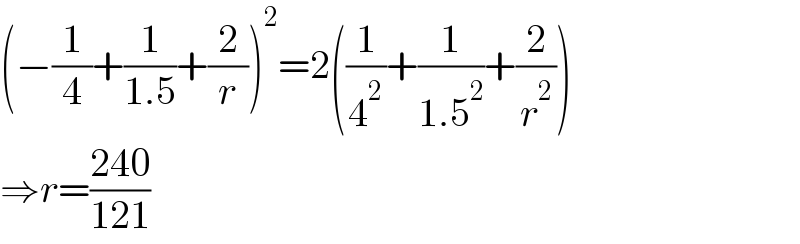
$$\left(−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{1}.\mathrm{5}}+\frac{\mathrm{2}}{{r}}\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{1}.\mathrm{5}^{\mathrm{2}} }+\frac{\mathrm{2}}{{r}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{r}=\frac{\mathrm{240}}{\mathrm{121}} \\ $$
