Question-185484

Question Number 185484 by Mingma last updated on 22/Jan/23

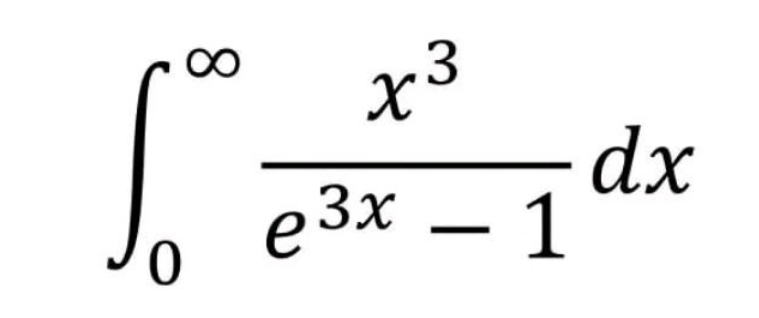
Answered by Ar Brandon last updated on 22/Jan/23

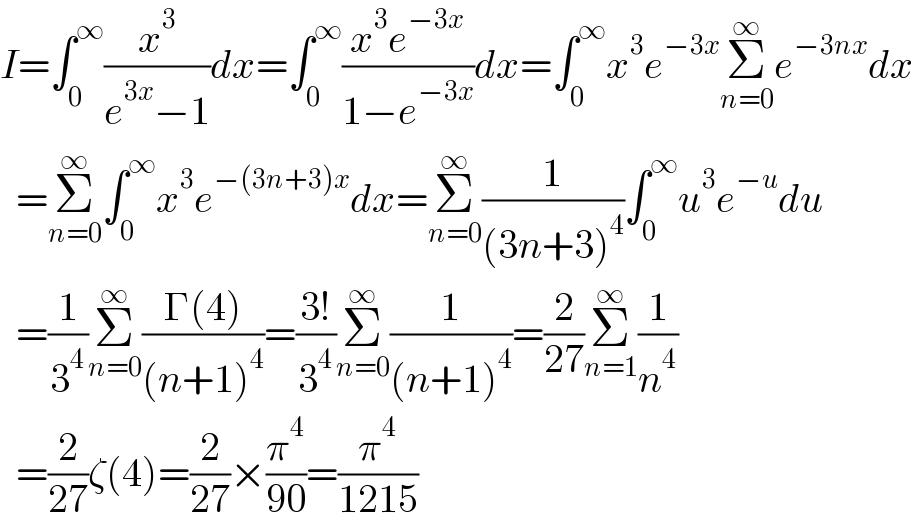
I=∫_0 ^∞ (x^3 /(e^(3x) −1))dx=∫_0 ^∞ ((x^3 e^(−3x) )/(1−e^(−3x) ))dx=∫_0 ^∞ x^3 e^(−3x) Σ_(n=0) ^∞ e^(−3nx) dx =Σ_(n=0) ^∞ ∫_0 ^∞ x^3 e^(−(3n+3)x) dx=Σ_(n=0) ^∞ (1/((3n+3)^4 ))∫_0 ^∞ u^3 e^(−u) du =(1/3^4 )Σ_(n=0) ^∞ ((Γ(4))/((n+1)^4 ))=((3!)/3^4 )Σ_(n=0) ^∞ (1/((n+1)^4 ))=(2/(27))Σ_(n=1) ^∞ (1/n^4 ) =(2/(27))ζ(4)=(2/(27))×(π^4 /(90))=(π^4 /(1215))

$${I}=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{3}} }{{e}^{\mathrm{3}{x}} −\mathrm{1}}{dx}=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{3}} {e}^{−\mathrm{3}{x}} }{\mathrm{1}−{e}^{−\mathrm{3}{x}} }{dx}=\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{3}} {e}^{−\mathrm{3}{x}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{e}^{−\mathrm{3}{nx}} {dx} \\ $$$$\:\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{3}} {e}^{−\left(\mathrm{3}{n}+\mathrm{3}\right){x}} {dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{3}\right)^{\mathrm{4}} }\int_{\mathrm{0}} ^{\infty} {u}^{\mathrm{3}} {e}^{−{u}} {du} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{4}} }\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\Gamma\left(\mathrm{4}\right)}{\left({n}+\mathrm{1}\right)^{\mathrm{4}} }=\frac{\mathrm{3}!}{\mathrm{3}^{\mathrm{4}} }\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{4}} }=\frac{\mathrm{2}}{\mathrm{27}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{4}} } \\ $$$$\:\:=\frac{\mathrm{2}}{\mathrm{27}}\zeta\left(\mathrm{4}\right)=\frac{\mathrm{2}}{\mathrm{27}}×\frac{\pi^{\mathrm{4}} }{\mathrm{90}}=\frac{\pi^{\mathrm{4}} }{\mathrm{1215}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply