Question Number 185495 by Mingma last updated on 22/Jan/23
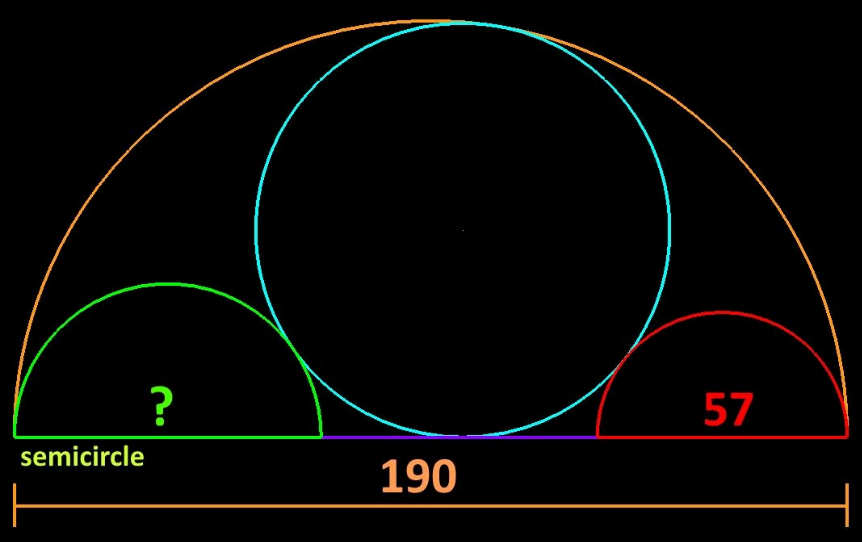
Answered by mr W last updated on 22/Jan/23

Commented by mr W last updated on 23/Jan/23

$$\left(−\frac{\mathrm{1}}{{R}}+\frac{\mathrm{2}}{{c}}+\frac{\mathrm{1}}{{r}}\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{{R}^{\mathrm{2}} }+\frac{\mathrm{2}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\right) \\ $$$$\frac{\mathrm{1}}{{r}^{\mathrm{2}} }−\left(\frac{\mathrm{4}}{{c}}−\frac{\mathrm{2}}{{R}}\right)\frac{\mathrm{1}}{{r}}+\frac{\mathrm{1}}{{R}}\left(\frac{\mathrm{1}}{{R}}+\frac{\mathrm{4}}{{c}}\right)=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}=\frac{\mathrm{4}}{{c}}−\frac{\mathrm{2}}{{R}} \\ $$$$\frac{\mathrm{1}}{{ab}}=\frac{\mathrm{1}}{{R}}\left(\frac{\mathrm{1}}{{R}}+\frac{\mathrm{4}}{{c}}\right)=\frac{\mathrm{1}}{{R}}\left(\frac{\mathrm{3}}{{R}}+\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}\right) \\ $$$$\Rightarrow\:\left({a}+{b}\right){R}+\mathrm{3}{ab}={R}^{\mathrm{2}} \\ $$$${example}: \\ $$$${R}=\mathrm{95} \\ $$$${b}=\mathrm{28}.\mathrm{5} \\ $$$$\Rightarrow{a}=\frac{\left({R}−{b}\right){R}}{{R}+\mathrm{3}{b}}=\frac{\left(\mathrm{95}−\mathrm{28}.\mathrm{5}\right)×\mathrm{95}}{\mathrm{95}+\mathrm{3}×\mathrm{28}.\mathrm{5}}=\mathrm{35} \\ $$$$?=\mathrm{2}{a}=\mathrm{70}\:\checkmark \\ $$
