Question Number 185542 by mathlove last updated on 23/Jan/23
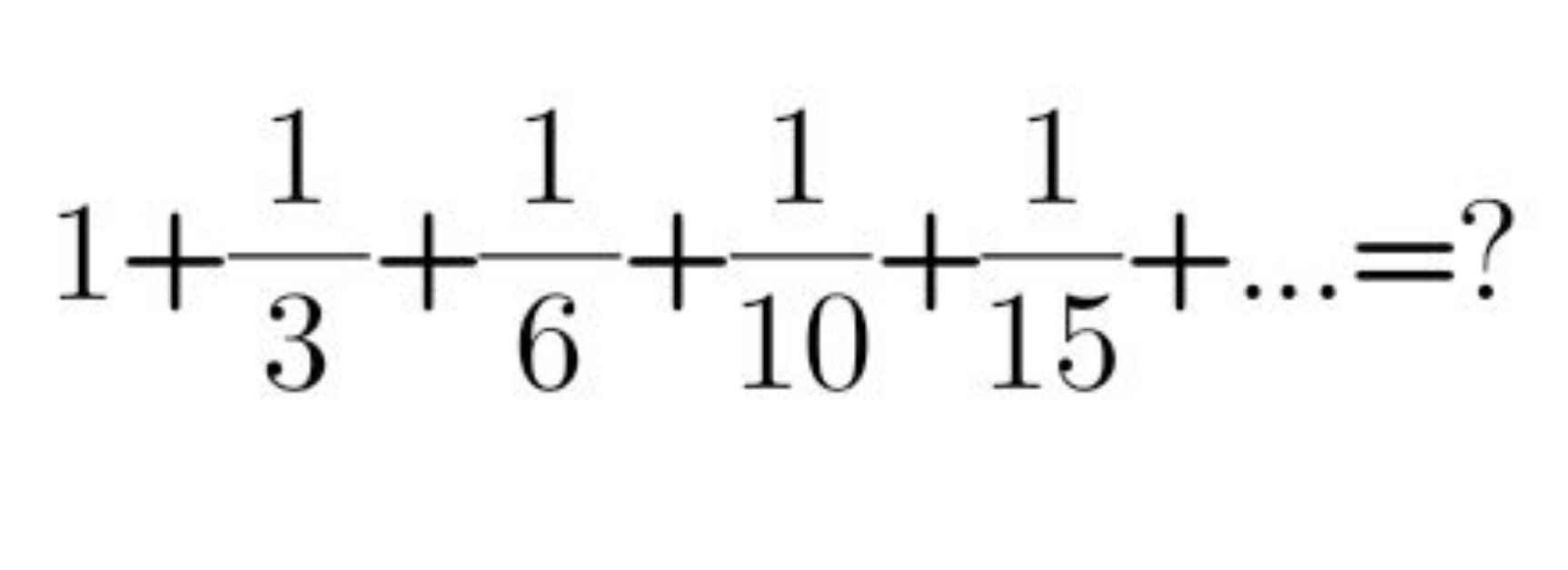
Answered by Ar Brandon last updated on 23/Jan/23
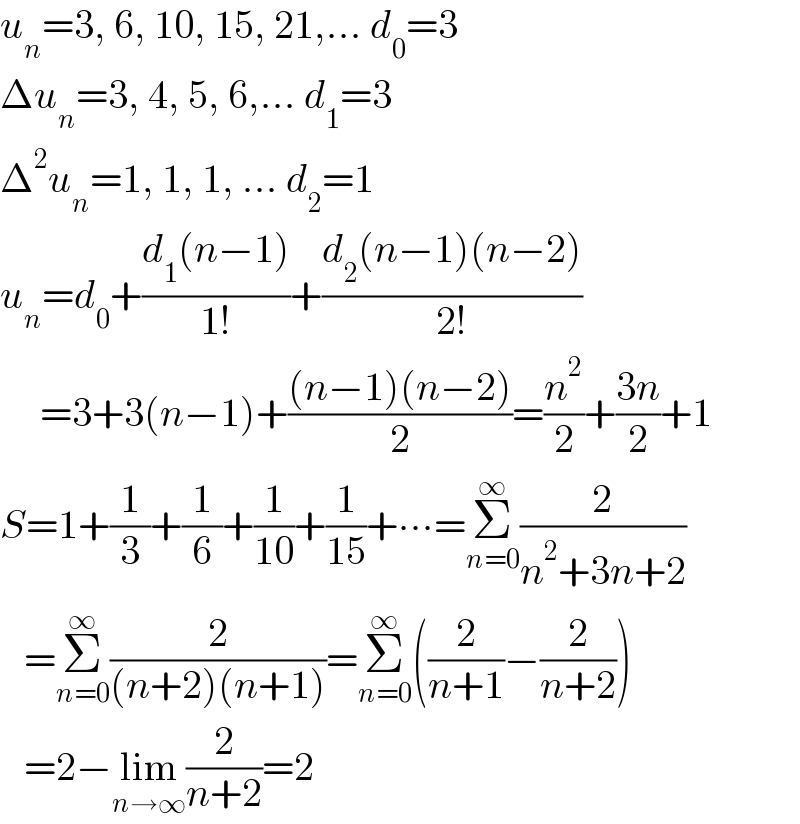
$${u}_{{n}} =\mathrm{3},\:\mathrm{6},\:\mathrm{10},\:\mathrm{15},\:\mathrm{21},…\:{d}_{\mathrm{0}} =\mathrm{3} \\ $$$$\Delta{u}_{{n}} =\mathrm{3},\:\mathrm{4},\:\mathrm{5},\:\mathrm{6},…\:{d}_{\mathrm{1}} =\mathrm{3} \\ $$$$\Delta^{\mathrm{2}} {u}_{{n}} =\mathrm{1},\:\mathrm{1},\:\mathrm{1},\:…\:{d}_{\mathrm{2}} =\mathrm{1} \\ $$$${u}_{{n}} ={d}_{\mathrm{0}} +\frac{{d}_{\mathrm{1}} \left({n}−\mathrm{1}\right)}{\mathrm{1}!}+\frac{{d}_{\mathrm{2}} \left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{2}!} \\ $$$$\:\:\:\:\:=\mathrm{3}+\mathrm{3}\left({n}−\mathrm{1}\right)+\frac{\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{2}}=\frac{{n}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{3}{n}}{\mathrm{2}}+\mathrm{1} \\ $$$${S}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{15}}+\centerdot\centerdot\centerdot=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}}{{n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{2}} \\ $$$$\:\:\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}}{\left({n}+\mathrm{2}\right)\left({n}+\mathrm{1}\right)}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{2}}{{n}+\mathrm{1}}−\frac{\mathrm{2}}{{n}+\mathrm{2}}\right) \\ $$$$\:\:\:=\mathrm{2}−\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}}{{n}+\mathrm{2}}=\mathrm{2} \\ $$
Commented by mathlove last updated on 23/Jan/23
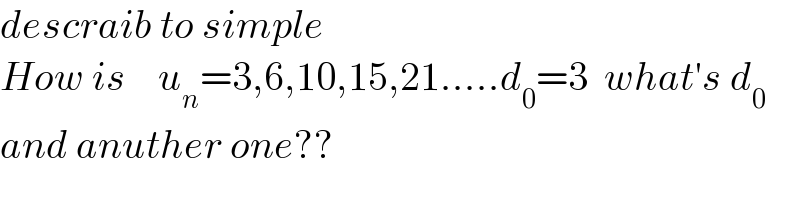
$${descraib}\:{to}\:{simple} \\ $$$${How}\:{is}\:\:\:\:{u}_{{n}} =\mathrm{3},\mathrm{6},\mathrm{10},\mathrm{15},\mathrm{21}…..{d}_{\mathrm{0}} =\mathrm{3}\:\:{what}'{s}\:{d}_{\mathrm{0}} \\ $$$${and}\:{anuther}\:{one}?? \\ $$
Commented by Ar Brandon last updated on 23/Jan/23
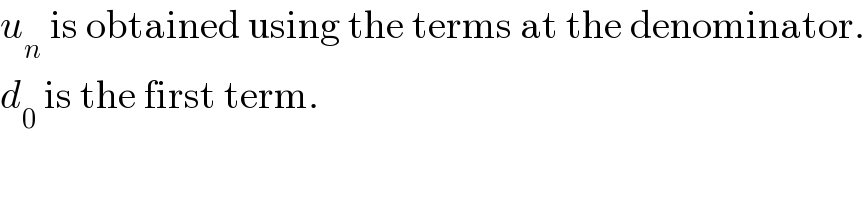
$${u}_{{n}} \:\mathrm{is}\:\mathrm{obtained}\:\mathrm{using}\:\mathrm{the}\:\mathrm{terms}\:\mathrm{at}\:\mathrm{the}\:\mathrm{denominator}. \\ $$$${d}_{\mathrm{0}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{first}\:\mathrm{term}. \\ $$
Answered by Frix last updated on 23/Jan/23

$${a}_{{n}} =\frac{\mathrm{2}}{{n}\left({n}+\mathrm{1}\right)} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k}} =\mathrm{2}−\frac{\mathrm{2}}{{n}+\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{2} \\ $$
