Question-185555

Question Number 185555 by yaslm last updated on 23/Jan/23

Answered by SEKRET last updated on 24/Jan/23

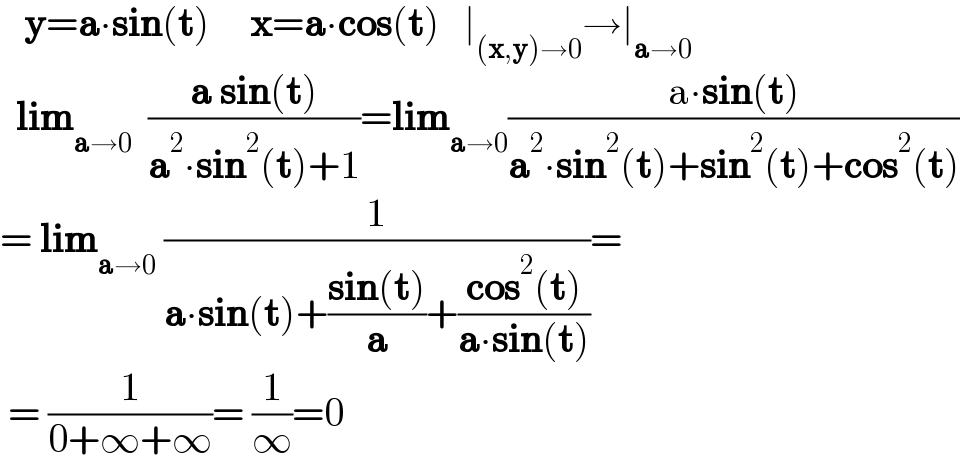
y=a∙sin(t) x=a∙cos(t) ∣_((x,y)→0) →∣_(a→0) lim_(a→0) ((a sin(t))/(a^2 ∙sin^2 (t)+1))=lim_(a→0) ((a∙sin(t))/(a^2 ∙sin^2 (t)+sin^2 (t)+cos^2 (t))) = lim_(a→0) (1/(a∙sin(t)+((sin(t))/a)+((cos^2 (t))/(a∙sin(t)))))= = (1/(0+∞+∞))= (1/∞)=0

$$\:\:\:\boldsymbol{\mathrm{y}}=\boldsymbol{\mathrm{a}}\centerdot\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{t}}\right)\:\:\:\:\:\boldsymbol{\mathrm{x}}=\boldsymbol{\mathrm{a}}\centerdot\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{t}}\right)\:\:\:\mid_{\left(\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}}\right)\rightarrow\mathrm{0}} \rightarrow\mid_{\boldsymbol{\mathrm{a}}\rightarrow\mathrm{0}} \\ $$$$\:\:\boldsymbol{\mathrm{lim}}_{\boldsymbol{\mathrm{a}}\rightarrow\mathrm{0}} \:\:\frac{\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{t}}\right)}{\boldsymbol{\mathrm{a}}^{\mathrm{2}} \centerdot\boldsymbol{\mathrm{sin}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{t}}\right)+\mathrm{1}}=\boldsymbol{\mathrm{lim}}_{\boldsymbol{\mathrm{a}}\rightarrow\mathrm{0}} \frac{\mathrm{a}\centerdot\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{t}}\right)}{\boldsymbol{\mathrm{a}}^{\mathrm{2}} \centerdot\boldsymbol{\mathrm{sin}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{t}}\right)+\boldsymbol{\mathrm{sin}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{t}}\right)+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{t}}\right)} \\ $$$$=\:\boldsymbol{\mathrm{lim}}_{\boldsymbol{\mathrm{a}}\rightarrow\mathrm{0}} \:\frac{\mathrm{1}}{\boldsymbol{\mathrm{a}}\centerdot\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{t}}\right)+\frac{\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{t}}\right)}{\boldsymbol{\mathrm{a}}}+\frac{\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{t}}\right)}{\boldsymbol{\mathrm{a}}\centerdot\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{t}}\right)}}= \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{0}+\infty+\infty}=\:\frac{\mathrm{1}}{\infty}=\mathrm{0}\:\: \\ $$

Commented by yaslm last updated on 24/Jan/23

nice, but I need delta , apselon

Answered by LEKOUMA last updated on 24/Jan/23

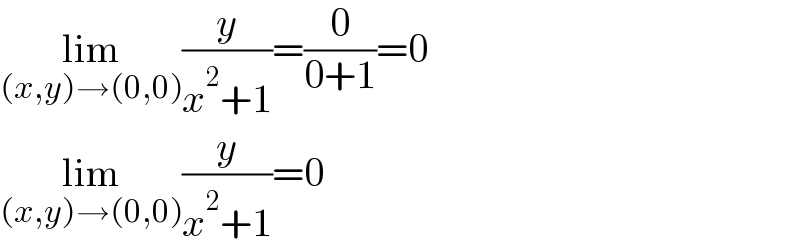
lim_((x,y)→(0,0)) (y/(x^2 +1))=(0/(0+1))=0 lim_((x,y)→(0,0)) (y/(x^2 +1))=0

$$\underset{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}}\frac{{y}}{{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{0}}{\mathrm{0}+\mathrm{1}}=\mathrm{0} \\ $$$$\underset{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}}\frac{{y}}{{x}^{\mathrm{2}} +\mathrm{1}}=\mathrm{0} \\ $$

Commented by yaslm last updated on 24/Jan/23

nice, but I need delta ,apselon

Answered by aba last updated on 29/Jan/23

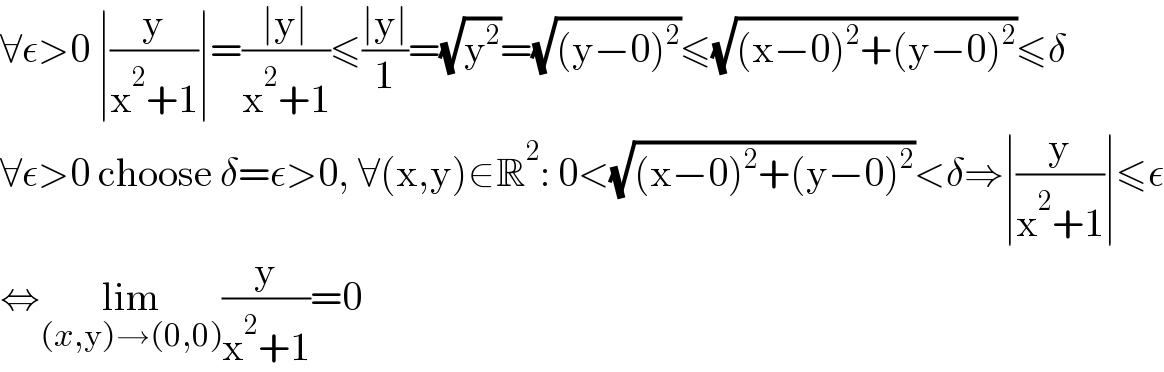
∀ε>0 ∣(y/(x^2 +1))∣=((∣y∣)/(x^2 +1))≤((∣y∣)/1)=(√y^2 )=(√((y−0)^2 ))≤(√((x−0)^2 +(y−0)^2 ))≤δ ∀ε>0 choose δ=ε>0, ∀(x,y)∈R^2 : 0<(√((x−0)^2 +(y−0)^2 ))<δ⇒∣(y/(x^2 +1))∣≤ε ⇔lim_((x,y)→(0,0)) (y/(x^2 +1))=0

$$\forall\epsilon>\mathrm{0}\:\mid\frac{\mathrm{y}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mid=\frac{\mid\mathrm{y}\mid}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\leqslant\frac{\mid\mathrm{y}\mid}{\mathrm{1}}=\sqrt{\mathrm{y}^{\mathrm{2}} }=\sqrt{\left(\mathrm{y}−\mathrm{0}\right)^{\mathrm{2}} }\leqslant\sqrt{\left(\mathrm{x}−\mathrm{0}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{0}\right)^{\mathrm{2}} }\leqslant\delta \\ $$$$\forall\epsilon>\mathrm{0}\:\mathrm{choose}\:\delta=\epsilon>\mathrm{0},\:\forall\left(\mathrm{x},\mathrm{y}\right)\in\mathbb{R}^{\mathrm{2}} :\:\mathrm{0}<\sqrt{\left(\mathrm{x}−\mathrm{0}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{0}\right)^{\mathrm{2}} }<\delta\Rightarrow\mid\frac{\mathrm{y}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mid\leqslant\epsilon \\ $$$$\Leftrightarrow\underset{\left({x},\mathrm{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}}\frac{\mathrm{y}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}=\mathrm{0} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply