Question Number 185557 by AROUNAMoussa last updated on 23/Jan/23
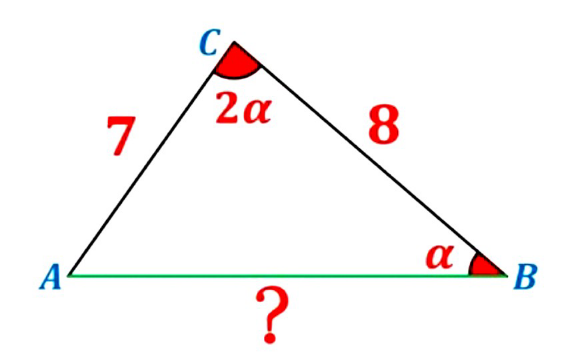
Commented by mr W last updated on 23/Jan/23

$${this}\:{is}\:{a}\:{copy}\:{of}\:{Q}\mathrm{180043} \\ $$
Commented by Frix last updated on 23/Jan/23
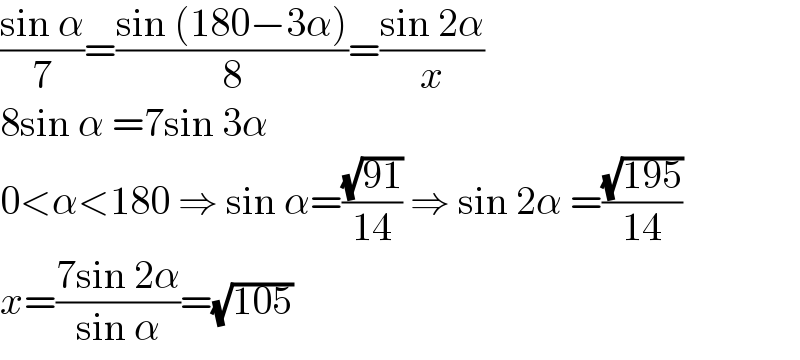
$$\frac{\mathrm{sin}\:\alpha}{\mathrm{7}}=\frac{\mathrm{sin}\:\left(\mathrm{180}−\mathrm{3}\alpha\right)}{\mathrm{8}}=\frac{\mathrm{sin}\:\mathrm{2}\alpha}{{x}} \\ $$$$\mathrm{8sin}\:\alpha\:=\mathrm{7sin}\:\mathrm{3}\alpha \\ $$$$\mathrm{0}<\alpha<\mathrm{180}\:\Rightarrow\:\mathrm{sin}\:\alpha=\frac{\sqrt{\mathrm{91}}}{\mathrm{14}}\:\Rightarrow\:\mathrm{sin}\:\mathrm{2}\alpha\:=\frac{\sqrt{\mathrm{195}}}{\mathrm{14}} \\ $$$${x}=\frac{\mathrm{7sin}\:\mathrm{2}\alpha}{\mathrm{sin}\:\alpha}=\sqrt{\mathrm{105}} \\ $$
Commented by SEKRET last updated on 23/Jan/23

$$\:\boldsymbol{\mathrm{hello}}\:\boldsymbol{\mathrm{sir}}\:\:\:\boldsymbol{\mathrm{W}}\:\:.\: \\ $$$$\:\: \\ $$How do you remember them?
Commented by mr W last updated on 23/Jan/23
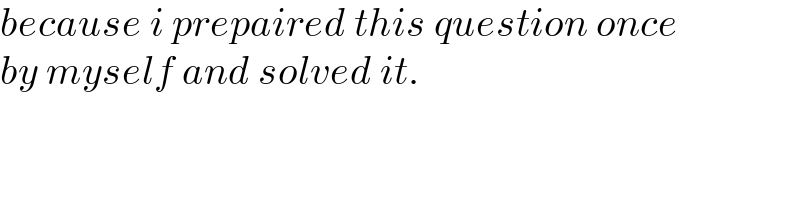
$${because}\:{i}\:{prepaired}\:{this}\:{question}\:{once} \\ $$$${by}\:{myself}\:{and}\:{solved}\:{it}. \\ $$
Commented by SEKRET last updated on 24/Jan/23

$$ \\ $$I was wondering why I didn't remember 😁
Answered by HeferH last updated on 23/Jan/23
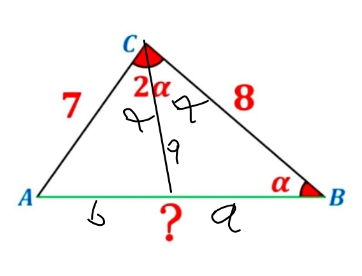
Commented by HeferH last updated on 23/Jan/23

$$\:\frac{\mathrm{7}}{{b}}\:=\:\frac{\mathrm{8}}{{a}} \\ $$$$\:{a}^{\mathrm{2}} =\:\mathrm{56}\:−\:{ab} \\ $$$$\:\frac{\mathrm{7}}{{b}}\:=\:\frac{\mathrm{8}}{{a}}\:\Rightarrow\:\:{b}\:=\:\frac{\mathrm{7}{a}}{\mathrm{8}}\: \\ $$$$\:{a}^{\mathrm{2}} \:=\:\mathrm{56}\:−\:\frac{\mathrm{7}{a}^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\:\mathrm{8}{a}^{\mathrm{2}} \:=\:\mathrm{448}\:−\:\mathrm{7}{a}^{\mathrm{2}} \\ $$$$\:{a}\:=\:\frac{\mathrm{8}\sqrt{\mathrm{105}}}{\mathrm{15}}\Rightarrow\:{b}\:=\:\frac{\mathrm{7}}{\mathrm{8}}\:\centerdot\:\frac{\mathrm{8}\sqrt{\mathrm{105}}}{\mathrm{15}}\:=\:\frac{\mathrm{7}\sqrt{\mathrm{105}}}{\mathrm{15}}\: \\ $$$$\:{a}\:+\:{b}\:=\:\:\frac{\mathrm{8}\sqrt{\mathrm{105}}}{\mathrm{15}}+\:\frac{\mathrm{7}\sqrt{\mathrm{105}}}{\mathrm{15}}\:=\:\frac{\mathrm{15}\sqrt{\mathrm{105}}}{\mathrm{15}}\:=\:\sqrt{\mathrm{105}} \\ $$
