Question Number 185580 by Shrinava last updated on 23/Jan/23
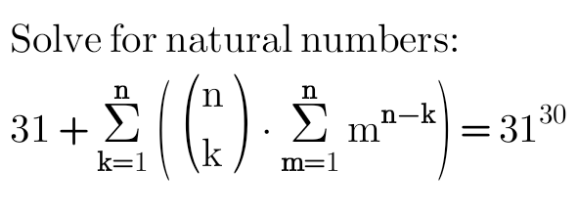
Answered by JDamian last updated on 24/Jan/23
![S=Σ_(k=1) ^n [ ((n),(k) ) ∙Σ_(m=1) ^n m^(n−k) ] =Σ_(k=1) ^n Σ_(m=1) ^n ((n),(k) )∙m^(n−k) =Σ_(m=1) ^n Σ_(k=1) ^n ((n),(k) )∙m^(n−k) =Σ_(m=1) ^n [(m+1)^n −m^n ]=(n+1)^n −1 31+(n+1)^n −1=31^(30)](https://www.tinkutara.com/question/Q185643.png)
$${S}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left[\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:\centerdot\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}{m}^{{n}−{k}} \right] \\ $$$$\:\:\:=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\centerdot{m}^{{n}−{k}} =\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\centerdot{m}^{{n}−{k}} \\ $$$$\:\:\:=\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\left[\left({m}+\mathrm{1}\right)^{{n}} −{m}^{{n}} \right]=\left({n}+\mathrm{1}\right)^{{n}} −\mathrm{1} \\ $$$$ \\ $$$$\mathrm{31}+\left({n}+\mathrm{1}\right)^{{n}} −\mathrm{1}=\mathrm{31}^{\mathrm{30}} \\ $$
Commented by Shrinava last updated on 24/Jan/23
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor},\:\mathrm{to}\:\mathrm{be}\:\mathrm{continued}? \\ $$
Commented by JDamian last updated on 25/Jan/23
![31+(n+1)^n −1=31^(30) (n+1)^n −1=31^(30) −31=31(31^(29) −1) [(n+1)^n −1]mod 31=31(31^(29) −1)mod 31=0 [(n+1)^n −1]mod 31=0](https://www.tinkutara.com/question/Q185683.png)
$$\mathrm{31}+\left({n}+\mathrm{1}\right)^{{n}} −\mathrm{1}=\mathrm{31}^{\mathrm{30}} \\ $$$$\left({n}+\mathrm{1}\right)^{{n}} −\mathrm{1}=\mathrm{31}^{\mathrm{30}} −\mathrm{31}=\mathrm{31}\left(\mathrm{31}^{\mathrm{29}} −\mathrm{1}\right) \\ $$$$\left[\left({n}+\mathrm{1}\right)^{{n}} −\mathrm{1}\right]\mathrm{mod}\:\mathrm{31}=\mathrm{31}\left(\mathrm{31}^{\mathrm{29}} −\mathrm{1}\right)\mathrm{mod}\:\mathrm{31}=\mathrm{0} \\ $$$$\left[\left({n}+\mathrm{1}\right)^{{n}} −\mathrm{1}\right]\mathrm{mod}\:\mathrm{31}=\mathrm{0} \\ $$
Commented by Shrinava last updated on 25/Jan/23
$$\mathrm{Ans}\:=\:\mathrm{0}\:\mathrm{dear}\:\mathrm{professor}? \\ $$
