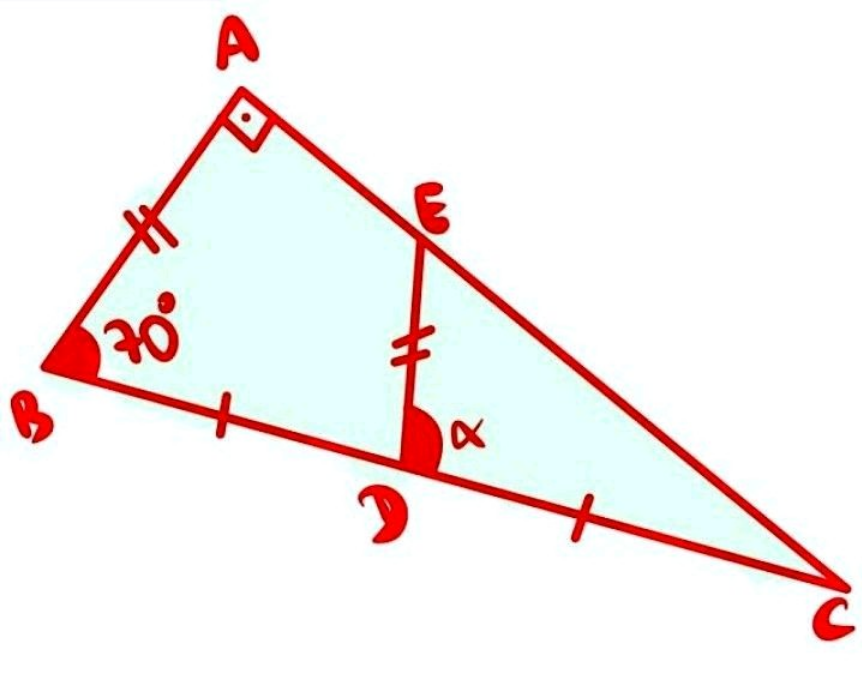
Question Number 185602 by Mingma last updated on 24/Jan/23
Answered by mr W last updated on 24/Jan/23
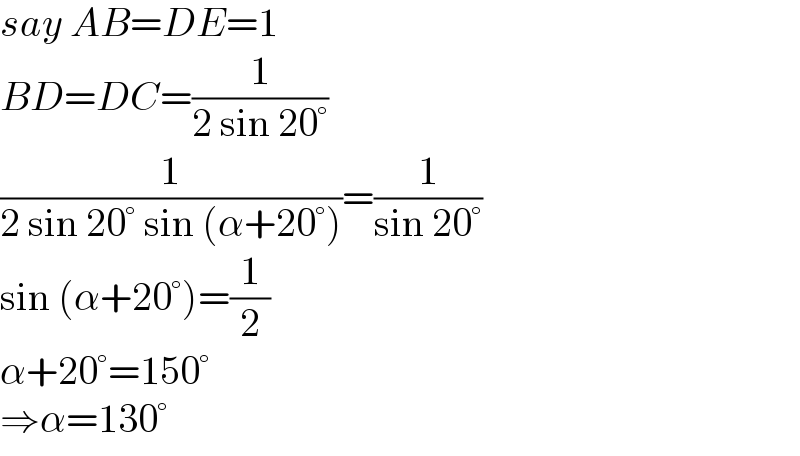
$${say}\:{AB}={DE}=\mathrm{1} \\ $$$${BD}={DC}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{20}°} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{20}°\:\mathrm{sin}\:\left(\alpha+\mathrm{20}°\right)}=\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{20}°} \\ $$$$\mathrm{sin}\:\left(\alpha+\mathrm{20}°\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\alpha+\mathrm{20}°=\mathrm{150}° \\ $$$$\Rightarrow\alpha=\mathrm{130}° \\ $$
Commented by malwan last updated on 24/Jan/23

$${great}\:{sir} \\ $$$${and}\:{sorry}\:{for}\:{my}\:{mistake} \\ $$
Answered by HeferH last updated on 24/Jan/23
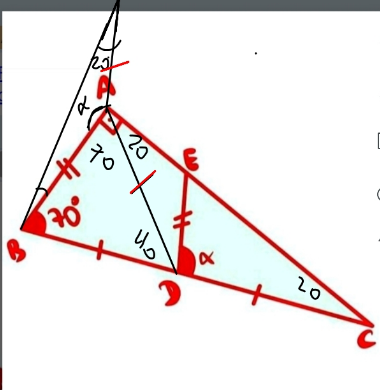
Commented by HeferH last updated on 24/Jan/23
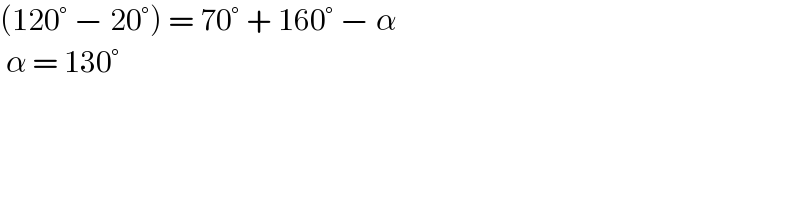
$$\left(\mathrm{120}°\:−\:\mathrm{20}°\right)\:=\:\mathrm{70}°\:+\:\mathrm{160}°\:−\:\alpha \\ $$$$\:\alpha\:=\:\mathrm{130}°\: \\ $$
