Question Number 185642 by Mingma last updated on 24/Jan/23
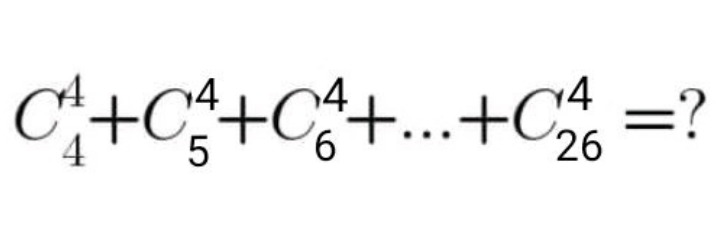
Commented by mr W last updated on 24/Jan/23

$$={C}_{\mathrm{4}+\mathrm{1}} ^{\mathrm{26}+\mathrm{1}} ={C}_{\mathrm{5}} ^{\mathrm{27}} =\mathrm{80730} \\ $$
Answered by cortano1 last updated on 25/Jan/23

$$\:\underset{{k}=\mathrm{4}} {\overset{{n}} {\sum}}\:{C}_{\mathrm{4}} ^{{k}} \:=\:\frac{\mathrm{1}}{\mathrm{4}!}\left(\frac{\left({n}−\mathrm{3}\right)\left({n}−\mathrm{2}\right)\left({n}−\mathrm{1}\right){n}\left({n}+\mathrm{1}\right)}{\mathrm{5}}\right)\: \\ $$
Commented by mr W last updated on 25/Jan/23

$$\:\underset{{k}=\mathrm{4}} {\overset{{n}} {\sum}}\:{C}_{\mathrm{4}} ^{{k}} \:=\:\frac{\mathrm{1}}{\mathrm{4}!}\left(\frac{\left({n}−\mathrm{3}\right)\left({n}−\mathrm{2}\right)\left({n}−\mathrm{1}\right){n}\left({n}+\mathrm{1}\right)}{\mathrm{5}}\right) \\ $$$$\:=\frac{\left({n}+\mathrm{1}\right)!}{\mathrm{5}!\left({n}−\mathrm{4}\right)!}={C}_{\mathrm{5}} ^{{n}+\mathrm{1}} \\ $$$${generally} \\ $$$$\underset{{k}={r}} {\overset{{n}} {\sum}}\begin{pmatrix}{{k}}\\{{r}}\end{pmatrix}\:=\begin{pmatrix}{{n}+\mathrm{1}}\\{{r}+\mathrm{1}}\end{pmatrix}\:{or}\:\underset{{k}={r}} {\overset{{n}} {\sum}}{C}_{{r}} ^{{k}} ={C}_{{r}+\mathrm{1}} ^{{n}+\mathrm{1}} \\ $$$${this}\:{is}\:{the}\:{Hockey}−{stick}\:{identity}. \\ $$
Commented by mr W last updated on 25/Jan/23

$${proof}\:{see}\:{Q}\mathrm{185659} \\ $$
