Question Number 185674 by ajfour last updated on 25/Jan/23
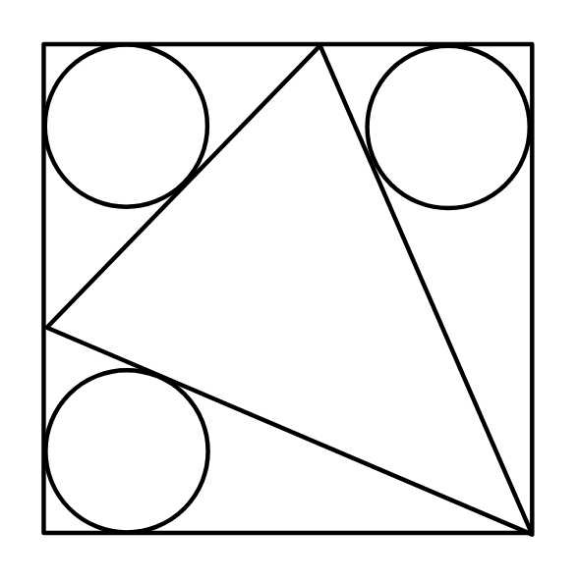
Commented by ajfour last updated on 25/Jan/23
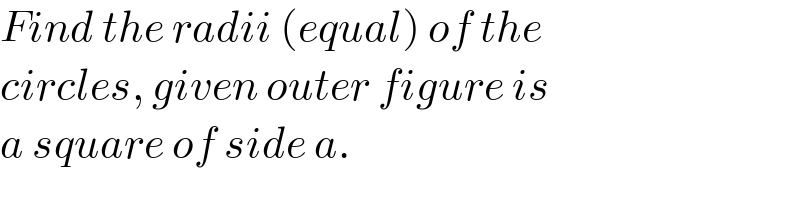
$${Find}\:{the}\:{radii}\:\left({equal}\right)\:{of}\:{the}\: \\ $$$${circles},\:{given}\:{outer}\:{figure}\:{is} \\ $$$${a}\:{square}\:{of}\:{side}\:{a}. \\ $$
Answered by mr W last updated on 25/Jan/23
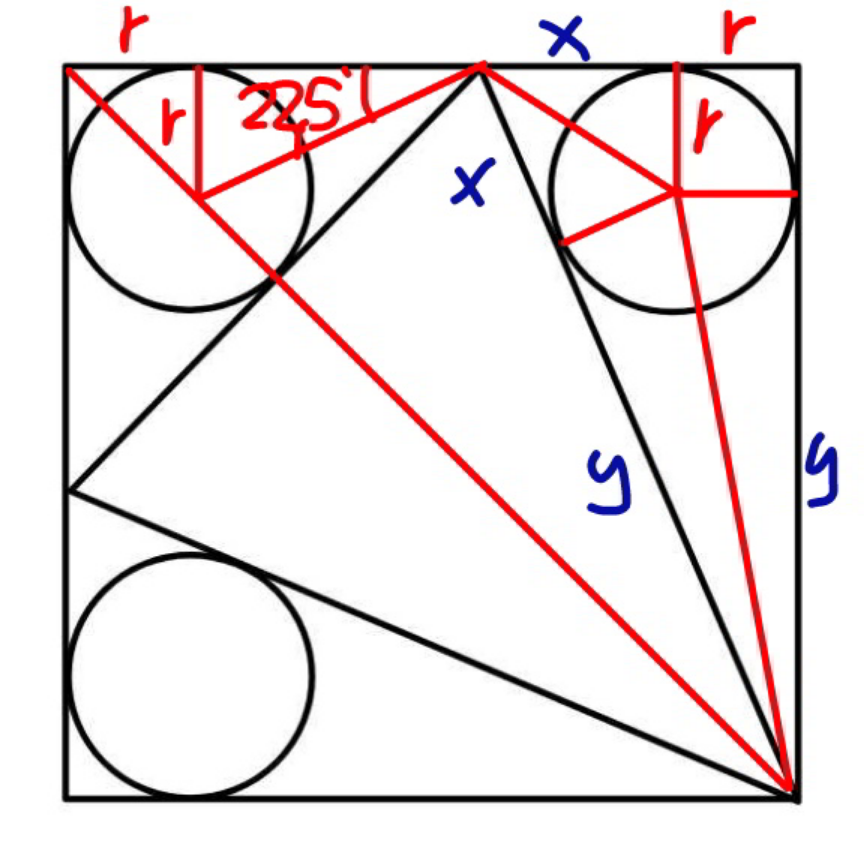
Commented by mr W last updated on 25/Jan/23
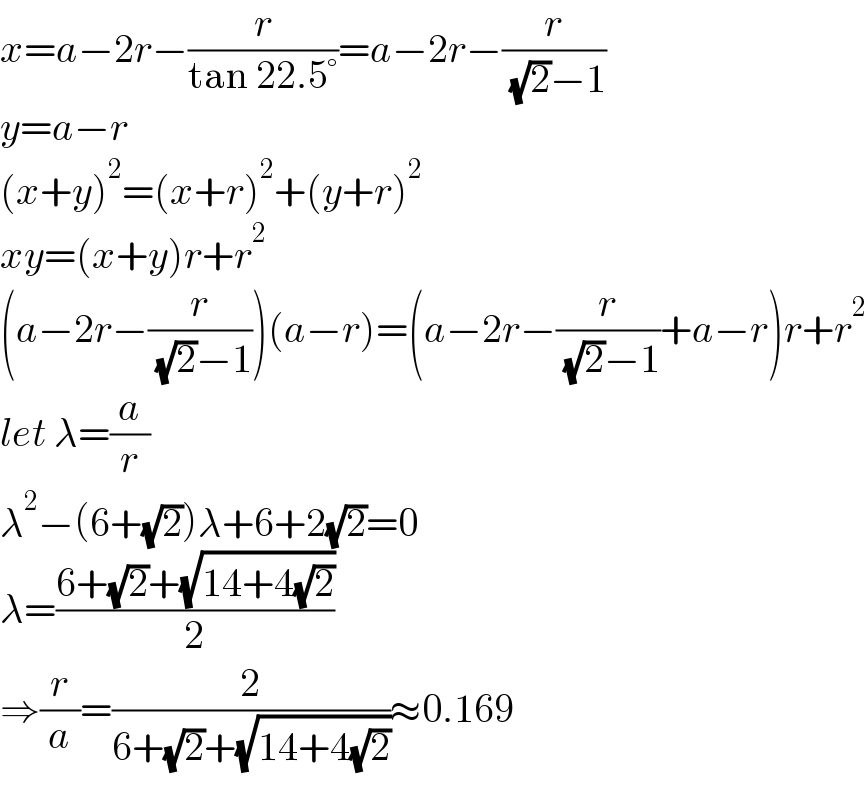
$${x}={a}−\mathrm{2}{r}−\frac{{r}}{\mathrm{tan}\:\mathrm{22}.\mathrm{5}°}={a}−\mathrm{2}{r}−\frac{{r}}{\:\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$${y}={a}−{r} \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} =\left({x}+{r}\right)^{\mathrm{2}} +\left({y}+{r}\right)^{\mathrm{2}} \\ $$$${xy}=\left({x}+{y}\right){r}+{r}^{\mathrm{2}} \\ $$$$\left({a}−\mathrm{2}{r}−\frac{{r}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right)\left({a}−{r}\right)=\left({a}−\mathrm{2}{r}−\frac{{r}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}+{a}−{r}\right){r}+{r}^{\mathrm{2}} \\ $$$${let}\:\lambda=\frac{{a}}{{r}} \\ $$$$\lambda^{\mathrm{2}} −\left(\mathrm{6}+\sqrt{\mathrm{2}}\right)\lambda+\mathrm{6}+\mathrm{2}\sqrt{\mathrm{2}}=\mathrm{0} \\ $$$$\lambda=\frac{\mathrm{6}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{14}+\mathrm{4}\sqrt{\mathrm{2}}}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{{r}}{{a}}=\frac{\mathrm{2}}{\mathrm{6}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{14}+\mathrm{4}\sqrt{\mathrm{2}}}}\approx\mathrm{0}.\mathrm{169} \\ $$
Commented by ajfour last updated on 27/Jan/23

$${Thank}\:{you}\:{sir}! \\ $$
