Question Number 185677 by Mingma last updated on 25/Jan/23
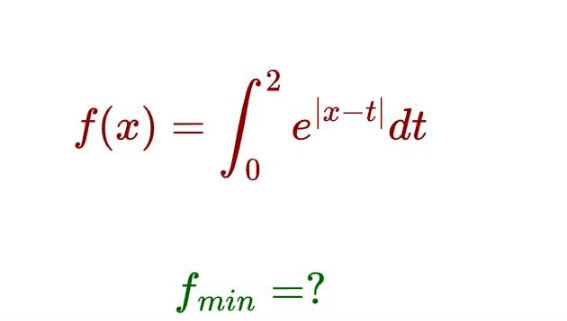
Answered by Frix last updated on 25/Jan/23
![(df/dx)=e^(∣x∣) −e^(∣x−2∣) =0 ⇒ x=1 f(1)=∫_0 ^2 e^(∣1−t∣) dt=2∫_0 ^1 e^(1−t) dt=2[−e^(1−t) ]_0 ^1 = =2(e−1)](https://www.tinkutara.com/question/Q185681.png)
$$\frac{{df}}{{dx}}=\mathrm{e}^{\mid{x}\mid} −\mathrm{e}^{\mid{x}−\mathrm{2}\mid} =\mathrm{0}\:\Rightarrow\:{x}=\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)=\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\mathrm{e}^{\mid\mathrm{1}−{t}\mid} {dt}=\mathrm{2}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\mathrm{e}^{\mathrm{1}−{t}} {dt}=\mathrm{2}\left[−\mathrm{e}^{\mathrm{1}−{t}} \right]_{\mathrm{0}} ^{\mathrm{1}} = \\ $$$$=\mathrm{2}\left(\mathrm{e}−\mathrm{1}\right) \\ $$
