Question Number 185768 by Mingma last updated on 27/Jan/23
Answered by JDamian last updated on 27/Jan/23

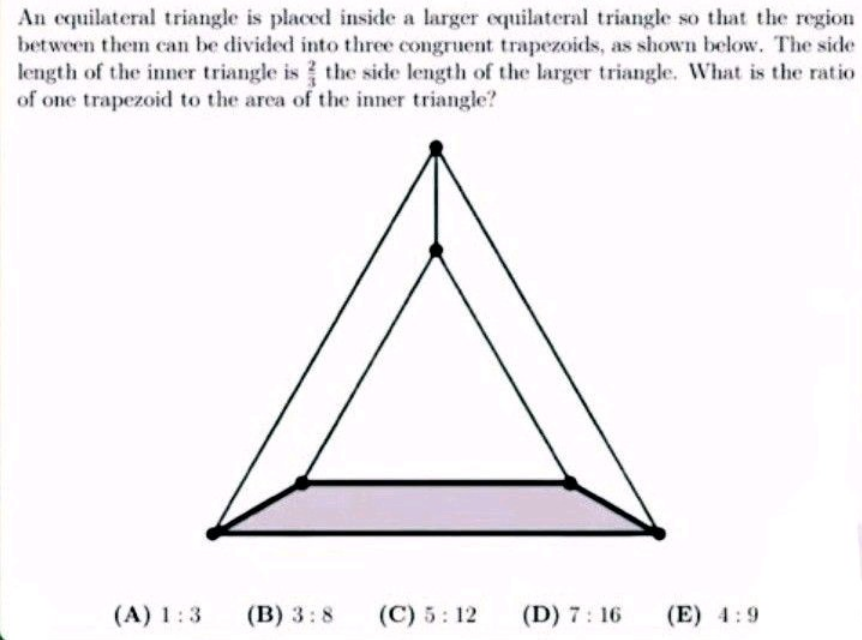
$${l}=\frac{\mathrm{2}}{\mathrm{3}}{L} \\ $$$$\mathrm{outer}\:\mathrm{triangle}\:\mathrm{area} \\ $$$$\:\:\:\:\:\:\:{A}={kL}^{\mathrm{2}} \\ $$$$\mathrm{inner}\:\mathrm{triangle}\:\mathrm{area} \\ $$$$\:\:\:\:\:\:\:\:\:{a}={kl}^{\mathrm{2}} ={k}\left(\frac{\mathrm{2}}{\mathrm{3}}{L}\right)^{\mathrm{2}} ={k}\frac{\mathrm{4}}{\mathrm{9}}{L}^{\mathrm{2}} \\ $$$$ \\ $$$$\frac{{A}}{{a}}=\frac{{kL}^{\mathrm{2}} }{{k}\frac{\mathrm{4}}{\mathrm{9}}{L}^{\mathrm{2}} }=\frac{\mathrm{9}}{\mathrm{4}}\:\:\Rightarrow\:\:{A}=\frac{\mathrm{9}}{\mathrm{4}}{a} \\ $$$$ \\ $$$$\mathrm{trapezoid}\:\mathrm{area} \\ $$$${s}=\frac{{A}−{a}}{\mathrm{3}}=\frac{\frac{\mathrm{9}}{\mathrm{4}}{a}−{a}}{\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{12}}{a} \\ $$$$ \\ $$$$\frac{{s}}{{a}}=\frac{\mathrm{5}}{\mathrm{12}} \\ $$
