Question Number 185770 by Mingma last updated on 27/Jan/23

Answered by mahdipoor last updated on 27/Jan/23
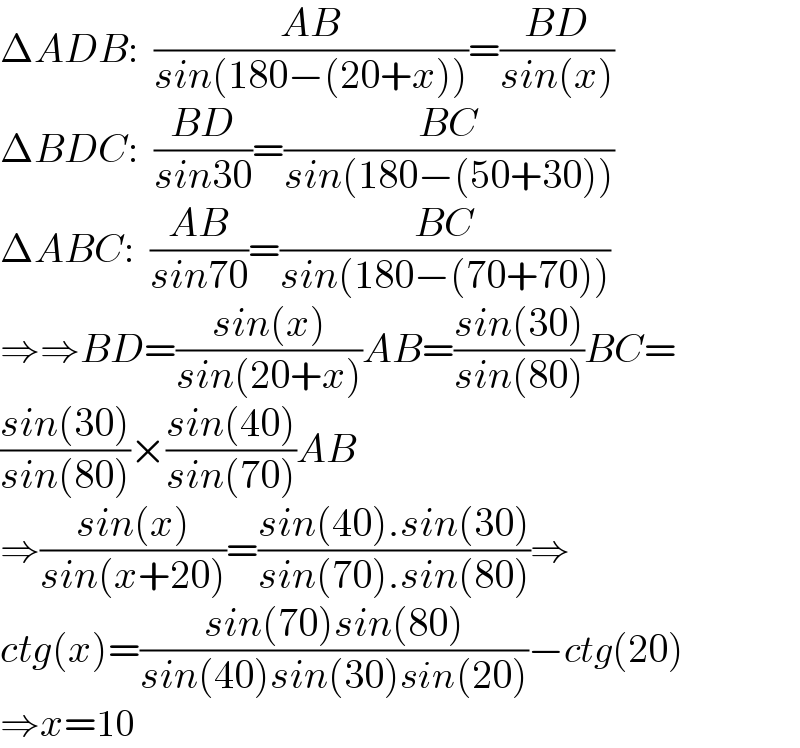
$$\Delta{ADB}:\:\:\frac{{AB}}{{sin}\left(\mathrm{180}−\left(\mathrm{20}+{x}\right)\right)}=\frac{{BD}}{{sin}\left({x}\right)} \\ $$$$\Delta{BDC}:\:\:\frac{{BD}}{{sin}\mathrm{30}}=\frac{{BC}}{{sin}\left(\mathrm{180}−\left(\mathrm{50}+\mathrm{30}\right)\right)} \\ $$$$\Delta{ABC}:\:\:\frac{{AB}}{{sin}\mathrm{70}}=\frac{{BC}}{{sin}\left(\mathrm{180}−\left(\mathrm{70}+\mathrm{70}\right)\right)} \\ $$$$\Rightarrow\Rightarrow{BD}=\frac{{sin}\left({x}\right)}{{sin}\left(\mathrm{20}+{x}\right)}{AB}=\frac{{sin}\left(\mathrm{30}\right)}{{sin}\left(\mathrm{80}\right)}{BC}= \\ $$$$\frac{{sin}\left(\mathrm{30}\right)}{{sin}\left(\mathrm{80}\right)}×\frac{{sin}\left(\mathrm{40}\right)}{{sin}\left(\mathrm{70}\right)}{AB} \\ $$$$\Rightarrow\frac{{sin}\left({x}\right)}{{sin}\left({x}+\mathrm{20}\right)}=\frac{{sin}\left(\mathrm{40}\right).{sin}\left(\mathrm{30}\right)}{{sin}\left(\mathrm{70}\right).{sin}\left(\mathrm{80}\right)}\Rightarrow \\ $$$${ctg}\left({x}\right)=\frac{{sin}\left(\mathrm{70}\right){sin}\left(\mathrm{80}\right)}{{sin}\left(\mathrm{40}\right){sin}\left(\mathrm{30}\right){sin}\left(\mathrm{20}\right)}−{ctg}\left(\mathrm{20}\right) \\ $$$$\Rightarrow{x}=\mathrm{10} \\ $$
